- Page 5, first displayed equations: add equation number (1)
-
Page 7, last sentence:
reference equation number (2) not (1)
CHAPTER 2
- Page 48, Example 2, Line 1: Omit the first occurrence of "single-precision" to read: "Determine the machine representation of the decimal number ..
-
[
Note: (Page 51, Line 3):
The IEEE Standard does not define the terms
{\bf machine epsilon} $(\epsilon)$ and {\bf unit roundoff error} $(u)$.
Frequently, they are used interchangeably or
some authors may define them as being different.
Machine epsilon is used to study the effect of
rounding errors because the actual errors of machine arithmetic are
extremely complicated. Program libraries may provide
precomputed values for these and other standard numerical quantites.
Often students are assigned the textbook exercise to compute
an approximate value for machine epsilon.
It is done in the sense of the spacing of the floating-point
numbers at 1 rather than in the sense of the unit roundoff error.
The following psuedo-code produces an approximation to machine
epsilon (within a factor of 2)
eps = 1.0
while (1.0 + eps > 1.0)
eps = eps/2.0
end
eps = 2.0*eps
As with any computational results, it depends on the particular computer platform used as well as the programming language, the floating-point format (float, double, long double, etc.), and the runtime library. ] -
Page 74, Computer Problem 19:
Change sign of the last term in the demoninator from plus to minus:
-28.17694u^6
CHAPTER 3
-
Page 87, Problem 3.1.21, Lines 1-2:
Replace $a \ge 2^m$ with $a = 2^m$ and
replace $m \le 0$ with $n \ge 24-m$
CHAPTER 4
- Page 127, Line 9: Omit $\ell_5$ to read: ...$\ell_3(x)$, and $\ell_4(x)$.
- Page 140, Line -3 above Figure 4.4: Should read: ... as shown in Figure 4.3.
- Page 144, Line -1 above pseudo-code: Replace subscript $0$ with subscript $n$ to read: ... to evaluate $P^n_n(t)$ when ...
- Page 144, Last line in pseudo-code: Replace subscript $0n$ with subscript $nn$ to read: \boldface{return} $S_{nn}$
- Page 154, Line +2 in Solution after FIGURE 4.6: Replace $(4,5)$ with $(4,6)$ to read: ... we added the points $(3,2)$, $(4,6)$, and $(1,12)$ ...
- Page 156, Figure 4.9: FIGURE 4.9, Label should read: Chebyhev nodes of $T_9$.
- Page 156, Figure 4.9: Change x-axis from -5 to 5 to -1 to 1.
- Page 156, Line 1, Should read: The Chebyshev nodes of $T_9$ are obtained by taking equally-spaced points on the unit circle and projecting them onto the horizontal axis, as in Figure 4.9.
-
Page 156, Figure 4.9:
Modify Figure 4.9 as shown below.
Leave center points above 0 and dashed line as is.
Move four points on right side of the semi-circle so that the
first four are equally spaced (20 degrees apart)
and the last one is half the distance (10 degrees),
with no point at the right end of the x-axis.
Repeat for the four points on the left side of the semi-circle.
Dashed lines and points on the x-axis are to be moved relative
to the above movement of points.
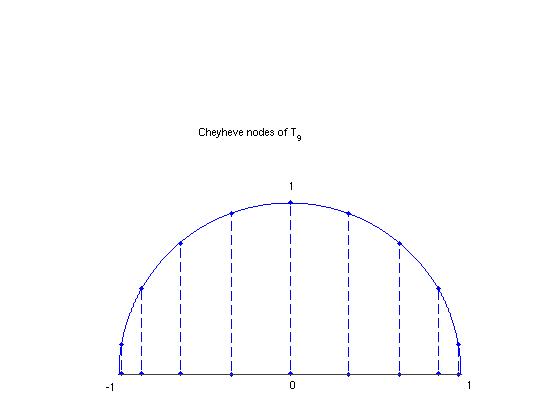
[ Note: Nine points on the semi-circle are not all evenly spaced but at 10, 30, 50, 70, 90, 110, 130, 150, 170 degress (counterclockwise). The points on the unit circle are $(\cos \theta, \sin \theta)$ with $\theta = (2i+1)\pi/18$ and $i=0,1,2,\ldots,8$.] - Page 167, 4th line from bottom: Replace $h^5$ by $h^6$
- Page 169, Algorithm 2, Step 4: Replace "0 \leq i" by "1 \leq i."
- Page 173, Line 5: Replace the superscript (v) by the superscript (5).
-
Page 175, Line 4:
Replace the superscript (v) by the superscript (5).
CHAPTER 5
- Page 198, first and third displayed equations: Replace h by n (four times).
- Page 201, Problem 5.2.17(d): Minus sign should be plus sign to read: $I(h)\approx h f(a) + \frac12 h^2 f'(a)$
-
Page 210, first table: $\phi$ should be $\varphi$.
CHAPTER 6
- Page 217, second displayed equation, insert missing "1 =" to read: $$\int_0^1 dx = 1 = A + B$$
- Page 218, Line 9: Linear mapping is missing an x. Should read: $y = \frac12(b-a)x + \frac12(a + b)$
- Page 219, first displayed equation, replace limits of integral -1 to 1 with 0 to 1
- Page 219, first three displayed equations, replace ds with dx.
- Page 234, Example 3, second = should be \approx
-
Page 235, THEOREM 2, WEIGHTED GAUSSIAN QUADRATURE THEOREM,
last displayed equation replace first $l_i$ with script $ell_i$
to match its second appearance in righthand integral.
CHAPTER 7
- Page 272, Line 8: Multiplier should be $a_{\ell_i, j}/a_{\ell_k, k)$ in both equations.
-
Page 274, Problem 13d:
Add symbol "a" indicating answer in back of book.
CHAPTER 8
- Page 333, line 6: Sentence not complete: add "is"
- Page 340, Problem 10, last line of coefficient matrix: Should be 4/3 -6 12
-
Page 341, Problem 11, last line of righthand-side matrix:
Should be 2.5
CHAPTER 9
-
Page 395, Example 14, line -2:
$\theta = i(\pi/12)$ should be $\theta = i(\pi/14)$
CHAPTER 13
-
Page 536, pseudocode Coarse_Check, Line 9, should be:
per = 100*real(m)/real(i)
CHAPTER 14
-
Page 571, Last Displayed Equation:
($1 \le n \le n-1$)
CHAPTER 16
-
Page 637, Problem 15d:
Add symbol "a" indicating answer in back of book.
ANSWERS
- Page 724, Solution Pb 1.1.8c: Replace 10 with 16, to read: p <- z^3(6 + z^4(9 + z^8(3 - z^{16})))
- Page 727, Solution Pb 3.1.21: Replace $n \ge 23$ with $n \ge 24-m$
- Page 731, Solution CPb 5.3.6: Insert minus signs to read: $-2/9 = -0.22222...$
-
Page 744, Problem B, 4g:
Should be $(63.72664)_8$
BIBLIOGRAPHY
-
Page 753, column 1:
van der Vorst should be lower case "v"
COVERS
- Inside back cover (left side), integral formulas. First $(a \neq 1)$ should be $(a \neq -1)$ and other two $(a \neq 1)$ yshould be $(a \neq 0)$
- Inside back cover (right side), line 5: smaller parens for $(x^2 < \pi^2/4)$
CHAPTER 1