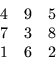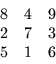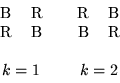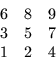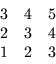Using Multicolor Orderings

For many iterative methods, the unknowns are updated in an order other than the natural (or lexicographical) ordering. The order in which the unknowns are updated can be specified by imposing a coloring on the mesh so that all the unknowns corresponding to nodes of a particular color are updated before the unknowns corresponding to nodes having a different color. Typically, a coloring is chosen so that unknowns (nodes) of the same color are decoupled, thus allowing these unknowns to be updated simultaneously. This property makes multicolor iterative methods especially attractive on vector or parallel computers.

NSPCG allows the matrix A to be reordered and permuted according to a coloring. The user can request that the matrix A be permuted before iterating by filling vector P in the NSPCG calling sequence with a coloring vector and setting IPERM [= IPARM(14)] to one. A coloring is defined as the assignment to each equation of an integer signifying the number of the color. If the mesh is to be colored with p colors, vector P contains for each equation an integer between 1 and p, inclusive. NSPCG will number those equations labeled with 1 first, followed by those equations labeled with 2, and so on. Equations labeled with p will be numbered last. NSPCG then permutes the matrix according to the new ordering of the equations before the iteration begins. After iteration has terminated, the matrix is permuted to its original form.

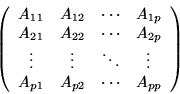
If a matrix whose mesh is colored with p colors is permuted according to the colors, the resulting matrix can be viewed as a p by p block matrix:

$$\left(\begin{array}{cccc} A_{11} & A_{12} & \cdots & A_{1p} ... ...ots \\ A_{p1} & A_{p2} & \cdots & A_{pp} \end{array} \right)$$

There are some restrictions on the use of permutations:

• If a permutation is requested with the primary storage format, the allowable preconditioners are SOR6, SSOR6, IC6, MIC6, and RS6. In this case, the coloring vector P must be chosen so that the diagonal block submatrices A_ii are diagonal. Thus, equations having the same color cannot be dependent. This requirement is made so that vectorization of these methods is possible. Otherwise, complicated block solves would be necessary for each diagonal block instead of a simple vector operation, and the primary storage format is not informative enough to vectorize such operations.
• If a permutation is requested with a diagonal storage format, the allowable preconditioners are SOR7, SSOR7, BIC7, BICX7, MBIC7, MBICX7, and RS7. In this case, the coloring vector P can be chosen so that the A_ii submatrices are banded. If they are banded, their bands must be dense.
• If a permutation is requested with a diagonal storage format, extra diagonals are often created. NSPCG will abort unless the column dimensions of the COEF and JCOEF arrays are set large enough to store the permuted matrix by diagonals.
• If a permutation is requested with a coordinate storage format, the allowable preconditioners are RICH5, JAC5, NEU5, and LSP5. There are no restrictions for permutations used with coordinate storage format, but permutations are not effective with these preconditioners.

When using the NSPCG package, the differences between ``block" and ``multicolor" methods are as follows:

1.

The name of a block preconditioner must end with a 2 or a 3, while the name of a multicolor preconditioner must end with a 6 or a 7.

2.

A multicolor preconditioner can only be applied after a permutation of the matrix (i.e., vector P must be set to a coloring vector and IPERM [= IPARM(14)] must be set to one). A block preconditioner can only be applied to a matrix which is not permuted by NSPCG.

3.

With a block method, the diagonal block matrices A_ii must be of equal size, which the user must specify with KBLSZ [= IPARM(19)]. With a multicolor method, the A_ii are not required to be of equal size.

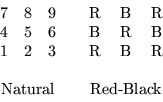
As an example of a coloring, suppose the user requests that a 3 by 3 mesh with the natural ordering be given a red-black ordering:

$$\begin{array}{cc} \begin{array}{ccc} 7 & 8 & 9 \\ 4 & 5 &... ...ular} \\ & \\ \mbox{Natural} & \mbox{Red-Black} \end{array}$$

If the red unknowns are to be labeled first, then P would be chosen as

P = ( 1, 2, 1, 2, 1, 2, 1, 2, 1)

resulting in the ordering:

$$\begin{array}{ccc} 4 & 9 & 5 \\ 7 & 3 & 8 \\ 1 & 6 & 2 \end{array}$$

If the user wished the black unknowns to be labeled first, P would be chosen as

P = ( 2, 1, 2, 1, 2, 1, 2, 1, 2)

resulting in the ordering:

$$\begin{array}{ccc} 8 & 4 & 9 \\ 2 & 7 & 3 \\ 5 & 1 & 6 \end{array}$$

If a preconditioner requires a permutation then the user must set IPERM [= IPARM(14)] equal to one and fill P with a coloring vector. There are two facilities in NSPCG for automatically generating coloring vectors -- REDBLK and COLOR.

1.

REDBLK determines whether or not matrix A has Property A. If it does, REDBLK generates a coloring vector for point red-black ordering. The calling sequence for REDBLK is

       CALL REDBLK (NDIM,N,MAXNZ,COEF,JCOEF,P,IP,NSTORE,IWKSP,IER)

The parameters NDIM, MAXNZ, COEF, JCOEF, N, and NSTORE have been explained previously. P, IP, and IWKSP are integer workspace vectors of length N on input. On output, P contains the coloring vector if IER =0. If IER =-8, the matrix does not have Property A, and a red-black coloring vector does not exist and the user must choose some other iterative method.

2.

COLOR replicates a rectangular (2-D) or box (3-D) color pattern throughout a rectangular or box domain. For example, a red-black pattern on a 2-D rectangular grid is a replication of the pattern:

$$\begin{tabular}{cc} B & R \\ R & B \end{tabular}$$

The calling sequence for COLOR is

       CALL COLOR (NXP,NYP,NZP,NX,NY,NZ,PATT,P)

NXP, NYP, and NZP are the x,y, and z dimensions of the pattern, and NX, NY, and NZ are the dimensions of the grid. For 2-D problems, NZP and NZ are both set to 1. PATT is an integer vector of length NXP*NYP*NZP containing the pattern in the order left-to-right, bottom-to-top. Different colors are coded as different integers in PATT, starting with one. P is an integer vector of length NX*NY*NZ which contains the coloring vector on output. For example, the color pattern

$$\begin{tabular}{cc} B & R \\ R & B \end{tabular}$$

would be specified with NXP =2, NYP =2, NZP =1, and PATT =(1,2,2,1). A red-black pattern in three dimensions whose pattern is given by

$$\begin{array}{cc} \begin{tabular}{cc} B & R \\ R & B \e... ... \\ B & R \end{tabular} \\ & \\ k=1 & k=2 \end{array}$$

would be specified with NXP =2, NYP =2, NZP =2, and PATT =(1,2,2,1,2,1,1,2). A line red-black pattern in two dimensions with the lines of the same color running horizontally as in the pattern

$$\begin{tabular}{c} B \\ R \end{tabular}$$

would be specified with NXP =1, NYP =2, NZP =1, and PATT =(1,2). The 4-color pattern in two dimensions

$$\begin{tabular}{cc} B & Y \\ R & G \end{tabular}$$

would be specified with NXP =2, NYP =2, NZP =1, and PATT =(1,2,3,4). A 4-color pattern is often applied to matrices resulting from a 9-point finite difference stencil.

There are many interesting colorings which cannot be generated by either REDBLK or COLOR since they do not represent replications of a rectangular pattern. One such coloring is ordering by diagonals along a rectangular mesh:

$$\begin{array}{ccc} 6 & 8 & 9 \\ 3 & 5 & 7 \\ 1 & 2 & 4 \end{array}$$

Such orderings are useful when the stencil is a 5-point star, because they allow vectorization along diagonals for such methods as SOR and IC(0). The coloring vector for such an ordering is

$$\begin{array}{ccc} 3 & 4 & 5 \\ 2 & 3 & 4 \\ 1 & 2 & 3 \end{array}$$

or

P = (1,2,3,2,3,4,3,4,5)