Left preconditioning is illustrated above. Many nonsymmetric
accelerators in the package allow other orientations for the
preconditioner, such as right preconditioning,
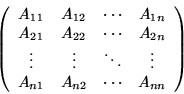
Let matrix A be written as

POINT PRECONDITIONERS
The point preconditioners available in the package are the
following:
LINE PRECONDITIONERS
![]()
The SOR iteration parameter ![]() can be determined by an
automatic adaptive procedure. This method allows no
acceleration.
can be determined by an
automatic adaptive procedure. This method allows no
acceleration.
![]()
SSOR iteration parameter ![]() can be determined by an
automatic adaptive procedure if SSOR is used with either
conjugate gradient or Chebyshev acceleration. Otherwise,
a user-supplied fixed
can be determined by an
automatic adaptive procedure if SSOR is used with either
conjugate gradient or Chebyshev acceleration. Otherwise,
a user-supplied fixed ![]() is required.
is required.
![]()
Case I occurs when matrix A has Property A (i.e., is 2-cyclic)
and k=0. Case II occurs if either condition fails.
Here, ![]() is a diagonal matrix containing the factorization
pivots, S is a strictly lower triangular matrix, and T is
a strictly upper triangular matrix.
It can be seen that if Case I is true, then a considerable
savings in storage is possible since only a vector of pivots
of length N has to be stored. Q can then be implicitly
represented from just
is a diagonal matrix containing the factorization
pivots, S is a strictly lower triangular matrix, and T is
a strictly upper triangular matrix.
It can be seen that if Case I is true, then a considerable
savings in storage is possible since only a vector of pivots
of length N has to be stored. Q can then be implicitly
represented from just ![]() and the given matrix elements,
which are already stored. If Case II is true, then
it is necessary to store T as well (and S, if A is
nonsymmetric).
A fill-in level of k=0 indicates that no fill-in beyond
the original matrix pattern of nonzeros is to be allowed
in the factorization. For k=1, fill-in resulting from
the original nonzero pattern is allowed but no fill-in
resulting from this newly-created fill-in is allowed. In
general, fill-in at level k results from fill-in from levels
and the given matrix elements,
which are already stored. If Case II is true, then
it is necessary to store T as well (and S, if A is
nonsymmetric).
A fill-in level of k=0 indicates that no fill-in beyond
the original matrix pattern of nonzeros is to be allowed
in the factorization. For k=1, fill-in resulting from
the original nonzero pattern is allowed but no fill-in
resulting from this newly-created fill-in is allowed. In
general, fill-in at level k results from fill-in from levels
![]() As k grows, the number of
iterations should decrease but at the expense of increased
storage and time per iteration.
As k grows, the number of
iterations should decrease but at the expense of increased
storage and time per iteration.
ILU(k) preconditioner
except that the diagonal pivots of the factorization are
adjusted so that Q-A has zero row sums. For many matrices,
this requirement produces a better condition number for
Q-1A than for the ILU(k) preconditioner. Also, this
requirement forces Q-1A to have at least one eigenvalue
equal to one. As in the previous preconditioner, a variable
level of fill-in is allowed.
![\begin{eqnarray*}A^{-1} & = & D^{-1}(I-CD^{-1})^{-1} \\
& = & D^{-1}[I+CD^{-1}+(CD^{-1})^2 + \cdots ]
\end{eqnarray*}](img27.gif)
A truncated form of this series is then used for Q-1.
Q-1 is not explicitly computed; Q-1p is
evaluated for a vector p by using a sequence of matrix-vector
multiplications. This method will be effective if the spectral
radius of CD-1 is less than one.
![]()
Since it is desired that the spectral radius of the iteration
matrix
G=I-Q-1A be small, ps is selected so that the
function
f(x)=1-ps(x)x has minimum 2-norm over a domain
which contains the spectrum of A. Note that G=f(A) is the
iteration matrix. This preconditioner is effective only if
A is SPD (symmetric and positive definite) or nearly so,
in which case, the domain is
![]() .
.
![]()
where DR and DB are diagonal matrices. This will only
be possible if matrix A has Property A [35]. The
black unknowns can be eliminated from the system to yield the
reduced system:
which becomes the new matrix problem to be solved. Once
uR has converged to an answer, uB is found by
The reduced system preconditioner is DR. Note that the
reduced system is not explicitly computed with this
method. However, NSPCG contains a facility for explicitly
computing the reduced system and applying any of the
package preconditioners to it. See Section 11
for more details.
The line preconditioners available in the package are the
following:
![]() ,
the block diagonal part
of A. For many matrices resulting from finite difference
discretizations of partial differential equations,
,
the block diagonal part
of A. For many matrices resulting from finite difference
discretizations of partial differential equations,
![]() is a tridiagonal matrix. The solution to the
preconditioning equation
is a tridiagonal matrix. The solution to the
preconditioning equation
![]() is accomplished by a recursive forward and back solve.
If, however,
is accomplished by a recursive forward and back solve.
If, however, ![]() consists of multiple independent
subsystems of size KBLSZ, NSPCG will perform each step
of the factorization and solution process across all
the subsystems in an independent manner. This method
will vectorize on computers allowing constant stride
vector operations.
consists of multiple independent
subsystems of size KBLSZ, NSPCG will perform each step
of the factorization and solution process across all
the subsystems in an independent manner. This method
will vectorize on computers allowing constant stride
vector operations.
![]() .
The solution of
.
The solution of
![]() is accomplished by
is accomplished by
![]()
where the ![]() operator indicates a truncation of the
matrix to a banded system. The variable LTRUNC [= IPARM(17)]
is used to determine the half-bandwidth to be used
in the truncation. If
operator indicates a truncation of the
matrix to a banded system. The variable LTRUNC [= IPARM(17)]
is used to determine the half-bandwidth to be used
in the truncation. If ![]() is diagonally dominant, then
the diagonals of
is diagonally dominant, then
the diagonals of
![]() decay at an exponential
rate the further the diagonal is away from the main diagonal.
Hence for diagonally dominant
decay at an exponential
rate the further the diagonal is away from the main diagonal.
Hence for diagonally dominant ![]() ,
a banded approximation
to the inverse of
,
a banded approximation
to the inverse of ![]() will suffice. Thus, the
preconditioning step has been changed from a solve to a
matrix-vector multiply, a vectorizable operation.
will suffice. Thus, the
preconditioning step has been changed from a solve to a
matrix-vector multiply, a vectorizable operation.
![]()
![]()
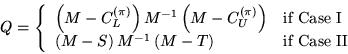
Case I occurs when matrix A has block Property A and no
fill-in of blocks is allowed. Case II occurs otherwise.
M here is a block diagonal matrix. Truncated inverses of
diagonal pivot block matrices are used in the construction
of the factorization. We illustrate the factorization
process in the case that A is block tridiagonal:
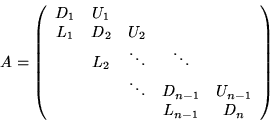
Then A has block Property A, so Case I is used. Thus we seek
a factorization of the form
![]()