COMMON MISTEAKS
MISTAKES IN
USING STATISTICS: Spotting and Avoiding Them
Frequentist Hypothesis Tests and p-values
As discussed on the page Overview
of Frequentist Hypothesis Tests, most commonly-used frequentist
hypothesis tests involve the following elements:
1. Model assumptions
2. Null and alternative hypothesis
3. A test statistic. This needs to have the property that
extreme values of the test statistic cast doubt on the null hypothesis.
4. A mathematical theorem saying, "If the model
assumptions and the null hypothesis are both true, then the sampling
distribution of the test statistic has this particular form."
The exact details of these four elements will depend on the particular
hypothesis test; see the page linked above for elaboration in the case
of the large sample z-test for a single mean.
The discussion on that page does not go into much detail on the concept
of sampling distribution.
This page will elaborate on that. First, read the page Overview
of Frequentist Confidence Intervals, which illustrates the idea of
sampling distribution for the sample mean. Then read
the following adaptation of that idea to the situation of a one-sided
t-test for a population mean.
This will illustrate the general concepts of of p-value and
hypothesis testing as well as sampling distribution for a hypothesis
test.
- We are considering a random variable Y which is
normally distributed. (This is one of the model assumptions.)
- Our null hypothesis
is: The population mean µ of
the random
variable Y is a certain value µ0.
- For simplicity, we will discuss a one-sided alternative hypothesis: The
population mean µ
of the random
variable Y is greater than µ0.
(i.e., µ >
µ0)
- Another model assumption says that samples are simple
random
samples. We have data in the form of a simple random
sample of size n.
- To understand the idea behind the hypothesis test, we
need to put our sample of data on hold for a while and
consider all possible simple
random samples of the same size n from the
random variable Y.
- For any such sample, we could calculate its
sample mean ȳ and its sample standard
deviation s.
- We could then use ȳ and
s to calculate the t-statistic t
= (ȳ - µ0)/(s/√n)
- Doing this for all possible simple random samples of
size n from Y gives us a new random variable, Tn. Its
distribution is
called a sampling distribution.
- The mathematical theorem associated with this
inference procedure (one-sided t-test for population mean) tells us
that if
the null hypothesis is true, then the sampling distribution has
what is called the t-distribution
with n degrees of freedom. (For large values of n, the
t-distribution looks very much like the standard normal distribution;
but as n gets smaller, the peak gets slightly smaller and the tails go
further out.)
- Now consider where
the t-statistic for the data at hand lies on the sampling distribution.
Two possible values are shown in red and green, respectively, in
the diagram below. Remember
that this picture depends on the validity of the model assumptions and
on the assumption that the null hypothesis is
true.
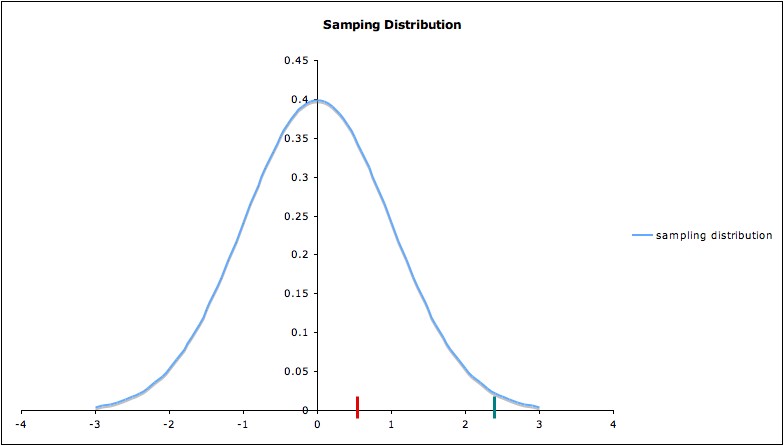
If the t-statistic lies at
the red bar (around 0.5) in the picture, nothing is surprising; our
data are consistent with the null hypothesis. But if the t-statistic
lies at the green bar (around 2.5), then the data would be fairly
unusual -- assuming the null hypothesis is true. So a t-statistic at the
green bar would cast some reasonable doubt on the null hypothesis.
A t-statistic even further to the right would cast even more doubt on
the null hypothesis.1
p-values
We can quantify the idea of how unusual a
test statistic is by the p-value.
The general definition is:
p-value = the probability of
obtaining a test statistic at least
as extreme as the one from the data
at hand, assuming the model assumptions and the null hypothesis are all
true.
Recall that we are only considering samples, from
the same random
variable, that fit the model
assumptions and of the same size as
the one we have. 2
So the definition of p-value, if we spell everything out, reads
p-value = the
probability of
obtaining a test statistic at least
as extreme as the one from the data
at hand, assuming
the model assumptions are all true, and the null hypothesis is true,
and the random variable is the same (including the same population),
and
the sample size is the same.
Comment:
The preceding discussion can be summarized as follows:
If we
obtain an unusually small p-value, then (at least) one of the following
must be true:
- At least one of the model assumptions is not true (in
which case the test may be inappropriate)
- The null hypothesis is false
- The sample we have obtained happens to be one of the
small percentage that result in a small p-value.
The interpretation of "at least as extreme as"
depends on the
alternative hypothesis:
- For the one-sided
alternative hypothesis µ > µ0
, "at least as extreme as" means "at least as great as". Recalling that
the probability of a random variable lying in a certain region is the
area under the probability distribution curve over that region, we
conclude that for this alternative hypothesis, the p-value is the area
under the distribution curve to the right
of the test statistic calculated from the data. (Note that, in
the picture, the p-value for the t-statistic at the green bar is much
less than that for the t-statistic at the red bar.)
- Similarly, for the other one-sided alternative µ< µ0 , the p-value is the area under
the distribution curve to the left
of the calculated test statistic. (Note that for this alternative
hypothesis, the p-value for the t-statistic at the green bar would be
much greater than the t-statistic at the red bar, but both would be
large as p-values go; in particular, the green value would be even more
unusual for this alternate hypothesis than for the null hypothesis.)
- For the two-sided alternative µ
≠ µ0, the p-value
would be the area under the curve to the right of the absolute value of
the
calculated t-statistic, plus the area under the curve to the left of
the negative of the absolute value of the calculated t-statistic.
(Since the sampling distribution in the illustration is symmetric about
zero, the two-sided p-value of, say the green value, would be twice the
area under the curve to the right of the green bar.)
Note that, for samples of
the same size2, the smaller the p-value, the stronger the
evidence against the null hypothesis, since a smaller p-value
indicates a more extreme test statistic. If the p-value is small enough
(and assuming all the model assumptions are met), rejecting the null hypothesis in favor of
the alternate hypothesis can be considered a rationale decision.
Comments:
- How small is "small enough" is a judgment call.
- "Rejecting the null hypothesis" does not mean the null hypothesis is
false or that the alternate hypothesis is true.
These comments are discussed further on the page Type I and II Errors.
1. A little algebra
will show that if
t
= (ȳ - µ0)/(s/√n)
is unusually large, then so is ȳ, and vice-versa.
2. Comparing p-values for samples of different size is a common
mistake. In fact, larger sample sizes are more likely to detect
a
difference, so are likely to result in smaller p-values than smaller
sample sizes, even though the context being examined is exactly the
same.
Last updated Jan 20, 2013

