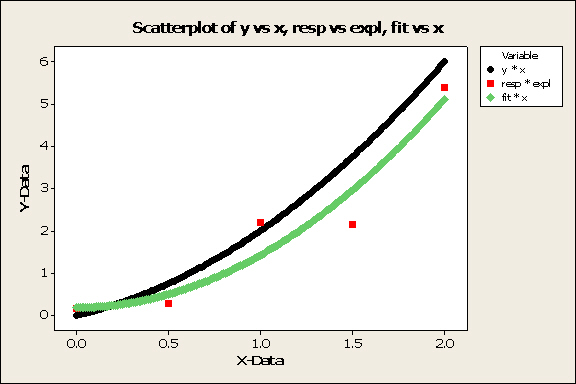
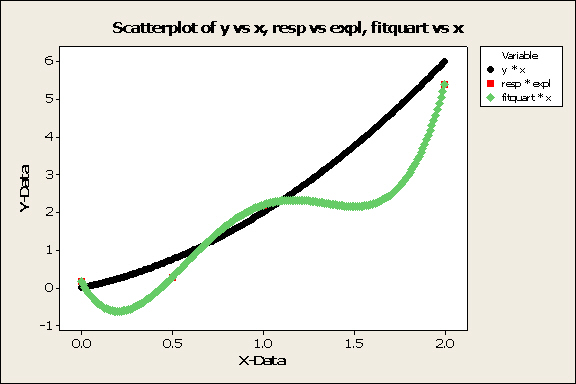
If you are gathering data
(especially through an experiment), be
sure to consult the literature on optimal design to plan the data
collection to get the tightest possible
estimates from the least amount of data.4
Unfortunately, there is not much known about sample sizes needed for
good modeling. Ryan5 quotes Draper and Smith6 as
suggesting that the number of observations should be at least ten times
the number of terms. Good and Hardin3 (p. 183) offer the
following
conjecture:
"If m points are
required to determine a univariate regression line with sufficient
precision, then it will take at least mn observations
and perhaps n!mn observations to
appropriately characterize and evaluate a regression model with n variables."