Some new geometric applications of quantum field theory
Andrew NeitzkeUniversity of Texas at Austin
Donaldson theory
A celebrated mathematical achievement of the 1980's: Donaldson's work on topology of 4-manifolds.

Key idea: given a $4$-manifold $M$, study self-dual Yang-Mills equations on $M$,
$$ (d A + A \wedge A)^- = 0 $$In this way Donaldson proved spectacular results, such as existence of compact topological 4-manifolds admitting no smooth structure.
He also obtained new invariants of 4-manifolds (integrals over space of solutions). But very difficult to compute!
Topological quantum field theory
Witten in 1988 realized that Donaldson's invariants of 4-manifolds are part of a much bigger structure:
A quantum field theory in $4$ dimensions, called "N=2 supersymmetric Yang-Mills theory with gauge group $SU(2)$."
I won't (can't) say exactly what a quantum field theory is. It's a description of possible laws of physics, in a hypothetical universe where spacetime dimension is $4$.
So, Donaldson's invariants of $4$-manifold $M$ are the outcomes of hypothetical experiments performed in a universe where $M$ is the spacetime.
So what?
What do we gain by taking Donaldson's concrete equations and embedding them into a far more complicated (and not mathematically rigorous) quantum field theory?
Not so much, until 1995.
Then a breakthrough in physics: Seiberg and Witten showed that at low energies this QFT reduces to something much simpler.
(Like describing $1$ kg of water by equations of hydrodynamics: this is much simpler than studying it as a system of $10^{26}$ interacting atoms!)
Seiberg-Witten theory
Seiberg-Witten showed that the QFT relevant for Donaldson theory can be reduced to essentially electromagnetism plus electrons.
This led to new Seiberg-Witten equations which are perfectly rigorous, predicted to capture the same information as the equations used by Donaldson, but are far easier to use. Major impact in 4-manifold topology (I'm told).
Differential equations
Now I'll apply the same philosophy to a different problem: linear differential equations on ${\mathbb R}$.
This too we can study by embedding it into quantum field theory: first in $2$ dimensions, then in $6$ dimensions.
Just as before, we'll see a complicated "high-energy" description replaced by a much simpler "low-energy" one.
This story is partly work in progress, drawing heavily on joint work (hep-th) with Davide Gaiotto and Greg Moore, and more recent work of Gaiotto.
Thanks also to Pietro Longhi and Chan Park, whose wonderful software "loom" I used in preparing figures.
Classical particle in 1 dimension
Consider a particle moving on the real line ${\mathbb R}$, subject to a force $F = - dV/dq$.
$V(q)$ is the potential. Say $V(q) \to \infty$ as $q \to \pm \infty$.
Phase space
At any time $t$, the particle has position $q \in {\mathbb R}$ and momentum $p = \dot{q} \in {\mathbb R}$.
The motion traces out a spectral curve in phase space ${\mathbb R}^2$:
$$ \Sigma = \left\{ \frac12 p^2 + V(q) = E \right\} \subset {\mathbb R}^2 $$Hamiltonian evolution
Hamiltonian evolution
$$ \dot{p} = - \partial_q H $$ $$ \dot{q} = \partial_p H $$where $$ H = \frac12 p^2 + V(q) $$
Captured by symplectic structure on phase space ${\mathbb R}^2$:
$$ \{ p, q \} = -\{ q, p \} = 1, \qquad \dot{f} = \{ H, f \} $$Spectral curve
Spectral curve $H = E$ is a Lagrangian submanifold of symplectic phase space.
(In a $2n$-dimensional phase space, "Lagrangian submanifold" means a submanifold given by vanishing of $n$ quantities $f_i$ with $\{f_i,f_j\} = 0$.)
A kind of classical avatar of a quantum state.Arnol'd, Weinstein, ...
Quantum particle in 1 dimension
Quantization: replace $p \to i \hbar \frac{\partial}{\partial q}$, so spectral curve
$$ \frac12 p^2 + V(q) - E = 0 $$becomes Schrodinger equation
$$ \left[ - \frac{\hbar^2}{2} \frac{\partial^2}{\partial q^2} + V(q) - E \right] \psi(q,\hbar) = 0 $$Leading order
Leading order in $\hbar$: can write solutions in the form
$$ \psi(q,\hbar) \sim \exp \left[ \frac{i}{\hbar} \int p\,dq \right] $$i.e. everything is determined by the geometry of the spectral curve inside of the phase-space
and the form $p \, dq$ on it.
Beyond leading order
Now we want to describe the exact behavior of the solutions,not only an approximation.
General philosophy in symplectic geometry: Lagrangian submanifolds shouldn't be studied by themselves.
Rather, they are boundary conditions for (pseudo)holomorphic discs; here maps $f: D \to {\mathbb R}^2$, holomorphic if we identify ${\mathbb R}^2 \simeq {\mathbb C}$. Gromov, Floer, Witten, ...
Another Lagrangian
Now fix $q_* \in {\mathbb R}$. Then there's another Lagrangian submanifold $L(q_*)$ of phase space given by $q = q_*$.
We will need to consider holomorphic discs with bipartite boundary, on $\Sigma$ and $L(q_*)$.
Complexifying
Turns out better to complexify phase space: take $(p,q) \in {\mathbb C}^2$
$$ \Sigma = \left\{ \frac12 p^2 + V(q) = E \right\}, \qquad L(q_*) = \left\{ q = q_* \right\} $$and look at holomorphic curves in ${\mathbb C}^2$ (but in a different complex structure) with boundary on $\Sigma$ and $L(q_*)$.
Beyond leading order
Now look at the set of all $q \in {\mathbb C}$ such that there is a holomorphic disc ending on $L_q \cup \Sigma$:
Three paths emanate from each turning point $q_0$ where $V(q_0) = E$.
Claim: this picture is the only extra ingredient you need, to answer any question about the Schrodinger equation.
Energy levels
For example: what are the allowed energy levels?
i.e. for which $(E,\hbar)$ does there exist solution $\psi(q)$ with
$$ \int_{-\infty}^\infty dq\,\lvert \psi(q) \rvert^2 < \infty $$This is a shooting problem: start with $\psi(q)$ which decays as $q \to -\infty$, evolve it, see if it also decays as $q \to +\infty$.
Bohr-Sommerfeld quantization condition
For the harmonic oscillator $V = \frac12 q^2$:
Start with exponentially decaying solution $\psi \sim e^{\frac{i}{\hbar} \int p \, dq}$ as $q \to -\infty$, look at how it evolves to $q \to +\infty$. Determined by a sum of paths on $\Sigma$: one "direct" plus two "detours" controlled by the holomorphic discs.
Requiring $\int_{\infty}^{-\infty} dq\,|\psi(q)|^2 < \infty$ means detour paths must cancel:
$${\mathcal X}_1(E,\hbar) + {\mathcal X}_2(E,\hbar) = 0$$Bohr-Sommerfeld quantization condition
In this example,
$${\mathcal X}_{loop}(E,\hbar) = e^{\frac{i}{\hbar} \oint p \, dq} $$Thus get Bohr-Sommerfeld quantization condition determining $E$:
$$\oint p \, dq = 2 \pi (n + 1/2) \hbar $$Exact Bohr-Sommerfeld quantization condition
For the quartic oscillator, $V = \lambda q^4 + \frac12 q^2$:
All these terms must cancel, giving exact relation
$${\mathcal X}_1(E,\hbar) + {\mathcal X}_2(E,\hbar) + {\mathcal X}_3(E,\hbar) + {\mathcal X}_4(E,\hbar) + {\mathcal X}_5(E,\hbar) = 0$$where each ${\mathcal X}_i \sim e^{\frac{1}{\hbar} \int p \, dq}$.
Spectral coordinates
To compute the functions ${\mathcal X}_\gamma$: extend to functions of complex $\hbar$.
This leads to 1-parameter families of networks, depending on phase of $\hbar$. Corresponds to studying discs which are holomorphic in different complex structures on ${\mathbb C}^2$.
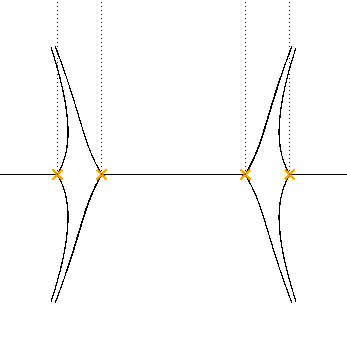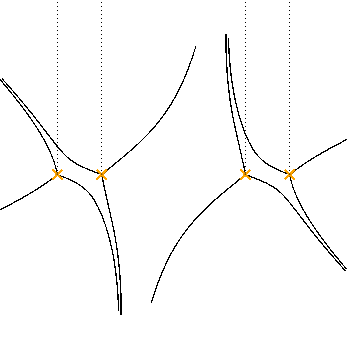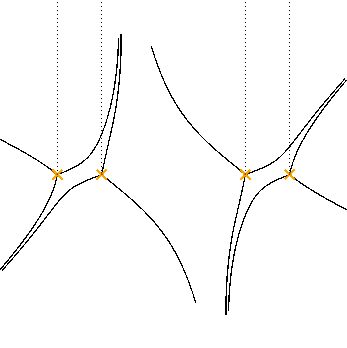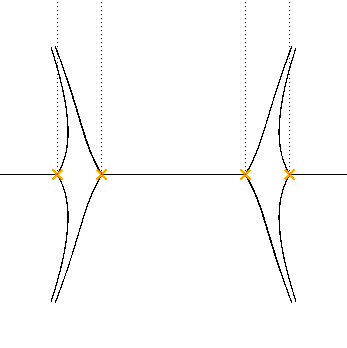
Saddle connections
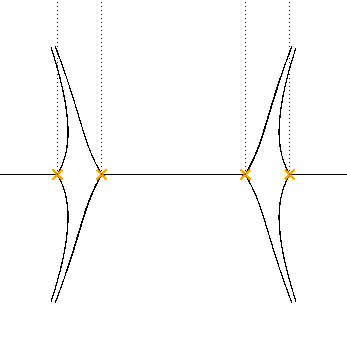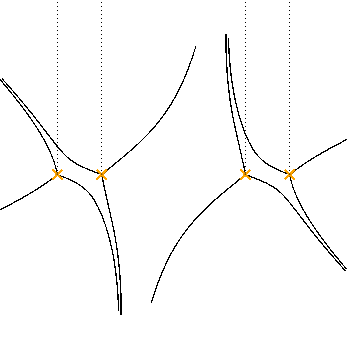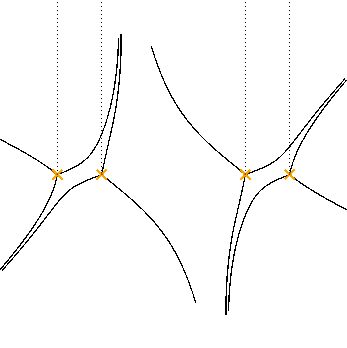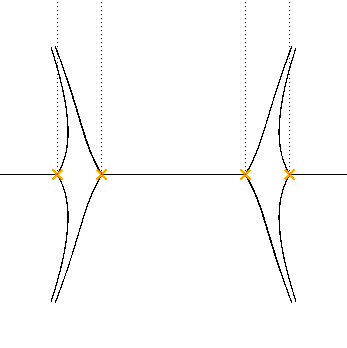
Topology of the network jumps when the phase of $\hbar$ crosses a critical value.
The jumps come from discs with boundary solely on $\Sigma$.
Analytic structure
${\mathcal X}_\gamma(\hbar)$ is piecewise analytic function of $\hbar$, with known discontinuities at the phases where holomorphic discs appear:
Also uniform asymptotics: ${\mathcal X_\gamma} \sim e^{\frac{i}{\hbar} \int p\,dq}$.
From these, plus boundedness as $\hbar \to \infty$, the ${\mathcal X}_\gamma(\hbar)$ for closed loops $\gamma$ are completely (and effectively) determined. Gaiotto-Moore-N, Gaiotto
Exact WKB method
All this can be thought of as an interpretation of the exact WKB method for degree $2$ scalar ODEs. Voros, Ecalle, Delabaere-Pham, ...
In that story one meets "Stokes graphs": locations where Borel summation of asymptotic series in $\hbar$ representing solutions breaks down.
Those Stokes graphs are just the pictures we have been drawing, determined by holomorphic discs!
Holomorphic cylinders
If we study equations with singularities we also get more exotic pictures, associated with the appearance of holomorphic cylinders rather than discs:

Higher degree equations
How about higher degree equations?
For degree $K$ we will have a parallel story, but now $\Sigma$ is a $K$-fold cover of ${\mathbb C}$ instead of $2$-fold.
The pattern of discs is more complicated: leads to walls which can intersect and give birth to new ones. Berk-Nevins-Roberts, Aoki-Kawai-Takei, Gaiotto-Moore-N, ...
Higher degree equations
e.g. for the equation
$$ \left[ \frac{\partial^3}{\partial q^3} + q \frac{\partial}{\partial q} + 1 \right] \psi(q) = 0 $$the spectral networks look like
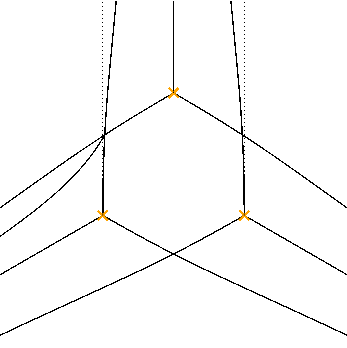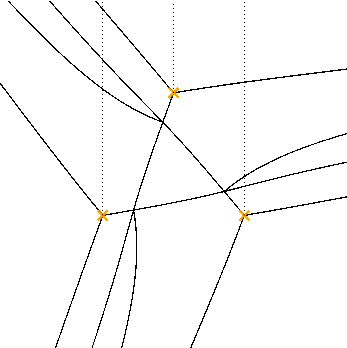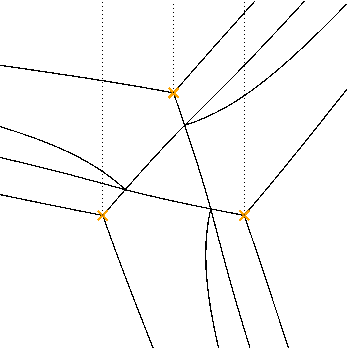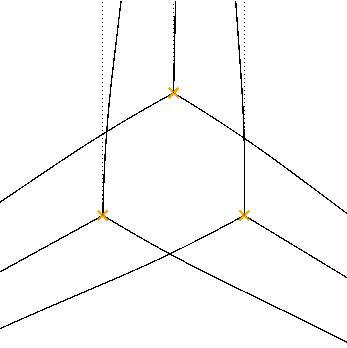
Tree appearing at critical phase, again represents holomorphic disc.
Higher degree equations
Another example:
$$ \left[ \frac{\partial^4}{\partial q^4} - 10 q \frac{\partial^2}{\partial q^2} + 4 \frac{\partial}{\partial q} + 9 z^2 \right] \psi(q) = 0 $$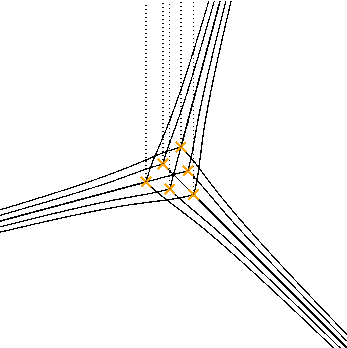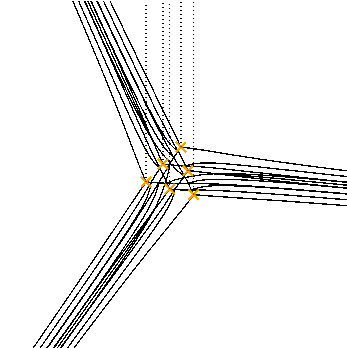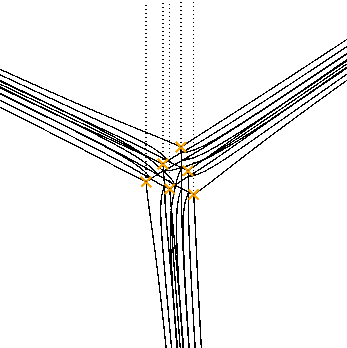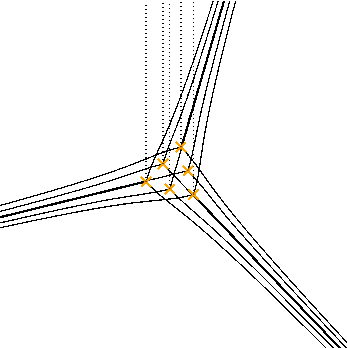
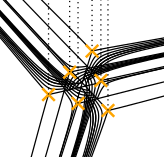
Complexity
It's not always so pretty: e.g. for the equation
$$ \left[ \frac{\partial^4}{\partial q^4} + (1+q^2) \frac{\partial^2}{\partial q^2} + \frac{\partial}{\partial q} + 1 \right] \psi(q) = 0 $$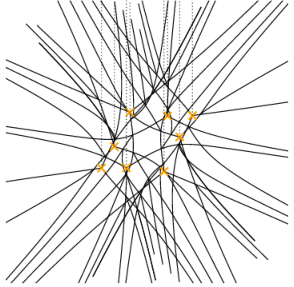
Tricky combinatorial problem to organize these pictures: conjecturally captured by cluster algebras. Fock-Goncharov, Gaiotto-Moore-N, Iwaki-Nakanishi, ...
Summing up
So far I described an approach to studying differential equations in one variable. The surprise was that holomorphic curves in complexified phase space were the key objects.
These holomorphic curves appear naturally as the spacetime in a $2$-dimensional quantum field theory ("A model"). Recently the idea that quantization should be studied via the A model has gained a lot of traction. Kapustin-Witten, Gukov-Witten, ... No doubt this story is related to that.
Closely related ideas have also appeared in the symplectic geometry literature. Nadler-Zaslow
But instead of pursuing that more, I want to switch to another place where these objects appeared: it involves field theory not in $2$ but in $6$ dimensions.
Nahm's classification
Werner Nahm asked (July 1977): which simple super Lie algebras could occur as the symmetry algebra of a quantum field theory?
Here is his answer:

An exceptional supersymmetry
The last entry on Nahm's list is particularly intriguing:
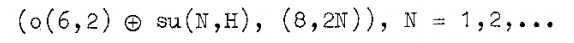
The first factor $o(6,2)$ is the Lie algebra of infinitesimal conformal transformations of six-dimensional Minkowski spacetime, ${\mathbb R}^{5,1}$.
So this algebra "wants to be" the symmetries of some quantum field theory in spacetime dimension six.
In 1977 this was "just" a curiosity: nobody knew how to make a nontrivial quantum field theory in spacetime dimension greater than four.
A stringy construction
Things changed with the advent of string theory. Here spacetime can be any 10-manifold with a metric obeying Einstein's equations (Ricci-flat).
Moreover spacetime is even allowed to have (some kinds of) singularities!
Type IIB string theory in spacetime $({\mathbb C}^2 / G) \times {\mathbb R}^{5,1}$:
with $G$ some finite subgroup of $SU(2)$.
Then there are some localized dynamics near the singularity at $0 \in {\mathbb C}^2 / G$, described by a six-dimensional QFT! Strominger, Witten 1995
Theory X
So, for every finite subgroup $G \subset SU(2)$, there is a six-dimensional quantum field theory ${\mathfrak X}_G$.
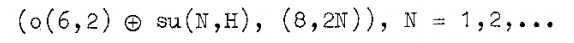
Theory ${\mathfrak X}_G$ realizes the exceptional superconformal symmetry discovered by Nahm (with $N=2$).
Theory ${\mathfrak X}_G$ is very different from the kinds of QFT treated in textbooks: no field quantization, no action principle, no perturbation theory, no Feynman diagrams, ...
Theory ${\mathfrak X}_G$ is also rigid: no free parameters!
Compactification
We can study the theory ${\mathfrak X}_G$ in various six-dimensional spacetimes.
For example, take a surface $C$ (with metric), and let spacetime be $C \times {\mathbb R}^{3,1}$.
Now take the limit where the volume of $C$ $\to 0$.
We obtain a QFT ${\mathfrak X}_G[C]$ on four-dimensional spacetime ${\mathbb R}^{3,1}$. Gaiotto-Moore-N
Genus of $C$ and moduli of the conformal structure of $C$ become parameters (couplings) of the field theory ${\mathfrak X}_G[C]$.
Theories of class S
Given a Riemann surface $C$, and a group $G \subset SU(2)$, we got a quantum field theory ${\mathfrak X}_G[C]$ in four dimensions. Now take $G = {\mathbb Z / K \mathbb Z}$.
Then theory ${\mathfrak X}_G[C]$ has to do with $K$-th order linear differential equations on the surface $C$. Gaiotto-Moore-N, Gaiotto
Let's describe some elements of the dictionary.
Vacua
Unlike the Standard Model (our universe), ${\mathfrak X}_G[C]$ has a degenerate vacuum: many possible configurations with zero energy.
The choice of a specific vacuum corresponds to the choice of a specific order $K$ differential equation to consider on $C$.
From now on, fix one.
Seiberg-Witten curves
The spectral curve $\Sigma$ is the "Seiberg-Witten curve" of the theory: its periods $\oint_\gamma p\, dq$ determine the low-energy couplings (electromagnetic interaction strengths).
Moral slogan: things on $C$ are high energy physics, things on $\Sigma$ are low energy physics. Low energy physics is much simpler, but map from high energy to low energy can be complicated.
Paths as interfaces
A path $\wp$ on the surface $C$ corresponds to an interface $I(\wp)$ between surface operators in the theory ${\mathfrak X}_G[C]$.

After factoring out the time direction, this interface looks like a bead on a string.

Framed BPS states

So we are studying a particle-like object $I(\wp)$ in our four-dimensional spacetime, corresponding to a path on $C$.
Then we can ask: what are the quantum ground states of this object? (Low energy physics.)
Framed BPS states
Recall each path $\wp$ on $C$ gets related to some collection of paths on the spectral curve $\Sigma$.
These paths correspond to the ground states of the interface. Their relative homology classes $\gamma$ give electromagnetic charges of the states.
Particles
The jumps of the networks, i.e. holomorphic curves ending on $\Sigma$, correspond to bulk particles in the 4-dimensional theory ${\mathfrak X}_G[C]$. (More precisely, to distinguished "BPS" states appearing in the 1-particle Hilbert space of the theory ${\mathfrak X}_G[C]$.)


The different types of jump correspond to particles with different properties, e.g. spin.
(On left: spin $1/2$, like electron; on right: spin $1$, like $W$ boson.)
What's it for?
We started with a question about differential equations living on a Riemann surface $C$.
Now we've "upgraded" to studying $4$-dimensional quantum field theory ${\mathfrak X}_G[C]$.
What do we gain from this maneuver (beyond what I already described)?
Structure in 4-dimensional field theory
More structure! All the objects in the theory can now move around in $4$-dimensional space. This leads to additional operations.
A concrete example: closed loops $\wp$ on $C$ correspond to line operators $L(\wp)$ in the theory ${\mathfrak X}_G[C]$.
This means there should be some monoidal category with distinguished objects corresponding to these loops. ("categorified skein algebra")
Local operators sitting on line operators give the morphisms. Bringing two line operators together in the $4$-dimensional space gives the monoidal structure.
Hitchin systems
The theory ${\mathfrak X}_G[C]$ perspective leads most directly to families of equations of the form
$$ \left[ \frac{\partial}{\partial z} + \frac{\varphi(z)}{\zeta} + A(z) \right] \psi(z) = 0, $$ $$ \left[ \frac{\partial}{\partial \bar{z}} + \zeta \varphi^\dagger(z) - A(z)^\dagger \right] \psi(z) = 0 $$where $\varphi(z)$, $A(z)$ are $K \times K$ matrices.
Note this problem is symmetric between $\zeta = 0$ and $\zeta = \infty$.
Studying this kind of family has an extra payoff: new information about hyperkahler metric on the Hitchin integrable system, e.g. asymptotic expansions of the metric around $\infty$.
Hitchin's integrable system is moduli space of vacua of the theory ${\mathfrak X}_G$ formulated on spacetime $C \times S^1 \times {\mathbb R}^{2,1}$.
Metric formulas for Hitchin systems
For example: conjecture asymptotic expansion of Kahler potential, giving metric on Teichmuller section of Hitchin integrable system for $G = SL(2)$,
$$ K = \underbrace{\frac{i}{4} \langle{Z,\bar{Z}}\rangle}_{\text{semiflat}} - \underbrace{\frac{1}{2 \pi^2} \Omega(\gamma_{min}) \sum_{n=1}^\infty |Z_{\gamma_{min}}| n\,K_1(2 \pi n |Z_{\gamma_{min}}|)}_{\text{from shortest finite saddle connection, } o\left(e^{-2 \pi |Z_{\gamma_{min}}|}\right)} + \underbrace{\cdots}_{\text{smaller as all } |Z_\gamma| \to \infty} $$where $Z_\gamma = \oint_\gamma p \, d q$, $\langle,\rangle$ is the intersection pairing, $\Omega(\gamma)$ counts saddle connections and closed loops in class $\gamma$, $K_1$ is Bessel function.
Intuitive idea: simple explicit term from simple low energy physics, receives complicated quantum corrections from the supersymmetric particles in the theory (saddle connections and closed loops).
Similar formula for higher rank, where $\Omega(\gamma)$ now counts all kinds of trees and worse degenerations.
Other uses of Theory X
So far: six-dimensional theory ${\mathfrak X}_G$ on the spacetimes $C \times {\mathbb R}^{3,1}$ or $C \times S^1 \times {\mathbb R}^{2,1}$ and their use in studying linear ODEs on $C$.
There are lots of other 6-manifolds out there! Putting theory ${\mathfrak X}_G$ on any of them seems to be related to interesting mathematics, e.g.:
taking the spacetime $M_3 \times S^3 / {\mathbb Z}_k$ is related to Chern-Simons invariants of $M_3$ (quantum topology), Dimofte-Gaiotto-Gukov
taking $T^2 \times C \times {\mathbb R}^{2}$ is related to the geometric Langlands program, Kapustin-Witten
taking $M_4 \times C$ is related to Donaldson/Seiberg-Witten invariants of 4-manifolds,
...? Probably much more to be discovered!
That's it
Thank you!Other uses of Theory X
A very optimistic diagram: