Preliminaries
Formulas for sampling with replacement (the
usual textbook formulas)
Formulas for sampling without replacement
Comparison and discussion
Reference: Mathematical Statistics and Data Analysis, John
A. Rice. Wadsworth, 1988, 1995. All proofs of the results for
sampling without replacement that are in these web pages are included
in the "Survey Sampling" chapter.
Preliminaries:
Assume that we have a population of size N. The values of the
population are numbers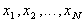 . When we take a
sample, it is a simple random sample (SRS) of size n, where
. When we take a
sample, it is a simple random sample (SRS) of size n, where
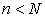 .
.
Population mean: 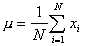
Population standard deviation: 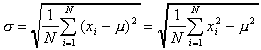
Unbiased estimator of the population mean (sample mean): 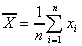
If the individual values of the population are "successes"
or "failures", we code those as 1 or 0, respectively.
Then the parameter of interest is usually called the population
proportion, even though, strictly speaking, it is also the population
mean.
Population proportion: 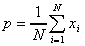
Population standard deviation: 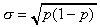
Unbiased estimator of the population proportion (sample proportion):
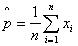
Return to the top.
If we assume the simple random sampling is with
replacement, then the sample values are independent, so the
covariance between any two different sample values is zero. This
fact is used to derive these formulas for the standard deviation
of the estimator and the estimated standard deviation of the estimator.
The first two columns are the parameter and the statistic which
is the unbiased estimator of that parameter.
| | standard deviation of the estimator
| usual estimator of the standard deviation of the estimator
|
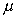 | 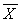
| 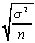 | 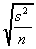 where where 
|
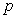 | 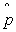
| 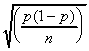 | 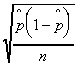
|
Return to the top.
If we assume the simple random sampling is without
replacement, then the sample values are not independent,
so the covariance between any two different sample values is not
zero. In fact, one can show that
Covariance between two different sample values: 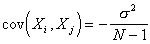 for
for 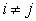
This fact is used to derive these formulas for the standard deviation
of the estimator and the estimated standard deviation of the estimator.
The first two columns are the parameter and the statistic which
is the unbiased estimator of that parameter.
| | standard deviation of the estimator
| estimator of the standard deviation of the estimator
|
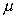 | 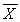
| 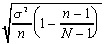 | 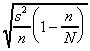 where where 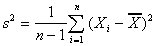
|
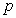 | 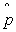
| 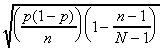 | 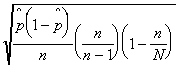
|
Return to the top.
Discussion:
- Notice that the main difference between the two sets of formulas
is the extra factor on each when we are sampling without replacement.
In each case, the extra factor is some number between 0 and 1,
so it makes the standard deviation smaller than it is for sampling
with replacement.
- If we actually do sampling without replacement (as we usually
do), but we analyze the results as if we sampled without replacement
(easier formulas that we all learned), how are our results in
error? (Answer: Our estimates of the standard deviation are a
little larger than they really should be, so we don't claim as
much accuracy in our estimators as we really should.)
- How much is the error? Answer: If the sample size is a lot
smaller than the population size, then the extra factor is really
close to 1, so there isn't much error. If the sample size is a
significant fraction of the population size, like half or so,
then the extra factor is about 0.70 (square root of ½). So
we really need to use the correct formula there to get reasonably
accurate results.
- In the textbook Basic Practice of Statistics, the author
(David Moore) says we can use the simple formulas for the standard
deviation as long as the population is at least 10 times as big
as the sample. If we use the simple formulas when the population
is exactly 10 times as big as the sample, how large is the factor?
(Answer: 0.95.) So how much off are we? (Answer: 5%) What if the
population is 20 times as big as the sample? (Answer: factor is
.975, for error of about 2.5%.)
- Why do we use the n-1 in the denominator of the estimator
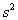 ? Answer: That's what it takes to make
this an unbiased estimator of
? Answer: That's what it takes to make
this an unbiased estimator of 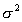 .
.
- Why isn't there an equivalent n-1 in a denominator
when we're estimating the variance of
 ?
Answer: Strictly speaking, there should be, if we were using exactly
as accurate mathematics in this case. However, because the numerators
here are very small, and usually the values of n are very
large, there is only a very tiny difference between using n
and n-1. Thus, most textbooks just put n here.
?
Answer: Strictly speaking, there should be, if we were using exactly
as accurate mathematics in this case. However, because the numerators
here are very small, and usually the values of n are very
large, there is only a very tiny difference between using n
and n-1. Thus, most textbooks just put n here.
- Do we always use unbiased estimators? Answer: No. Part of
the mathematics we learn to do in M378K is about proving which
estimators are unbiased. And we find that sometimes slightly biased
estimators are even better than strictly unbiased ones. What do
we mean by better? That they have smaller Mean Squared Error (MSE).
One of the main topics of a theoretical mathematical statistics
class is the theory of estimation. So if you want to really learn
about how to determine which estimators are better, you should
take M378K. In introductory courses, you have to just take the
word of the statisticians about which estimators people have found
to be most useful.
Return to the top.
Mary Parker
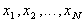 . When we take a
sample, it is a simple random sample (SRS) of size n, where
. When we take a
sample, it is a simple random sample (SRS) of size n, where
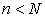 .
.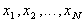
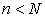
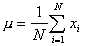
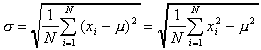
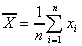
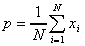
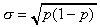
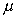
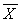
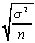
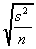 where
where 
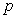
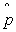
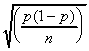
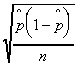
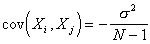
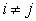
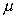
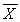
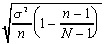
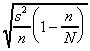 where
where 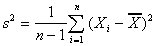
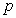
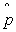
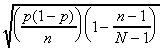
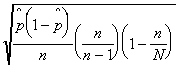
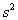 ? Answer: That's what it takes to make
this an unbiased estimator of
? Answer: That's what it takes to make
this an unbiased estimator of 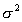 .
.
 ?
Answer: Strictly speaking, there should be, if we were using exactly
as accurate mathematics in this case. However, because the numerators
here are very small, and usually the values of n are very
large, there is only a very tiny difference between using n
and n-1. Thus, most textbooks just put n here.
?
Answer: Strictly speaking, there should be, if we were using exactly
as accurate mathematics in this case. However, because the numerators
here are very small, and usually the values of n are very
large, there is only a very tiny difference between using n
and n-1. Thus, most textbooks just put n here.