1. Consider the function
a) Find f'(x).
Soln: 
b) Find the slope of the line tangent to the curve y=f(x) at x=0.
Soln: Slope equals 
c) Find the equation of this tangent line.
Soln: Since f(0)=1, the tangent line is y-1 = 2.4(x-0), or y = 2.4 x + 1.
d) Use this tangent line to approximate f(0.01).
Soln: So f(0.01) is very close to 2.4(0.01) + 1 = 1.024.
2. From the following table, estimate f'(1). Indicate clearly how you obtain your answer:
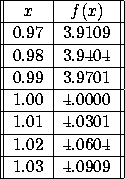
Solution: For h ranging from -.03 to +0.03, look at [f(1+h)-f(1)]/h:
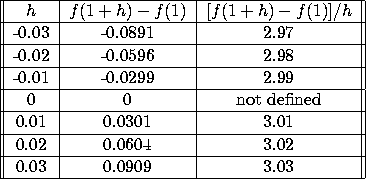
As h approaches zero from either side, [f(1+h)-f(1)]/h approaches 3, so f'(1) equals 3.
3. Evaluate the following limits, if they exist (or write DNE if they do not).
a)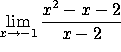 
As 
, the numerator goes to zero while the denominator goes to -3, so the ratio
goes to zero.
b)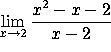 
As 
both the numerator and denominator go to zero, so we have to be more careful.
The numerator equals (x-2)(x+1). Canceling a factor of (x-2)
from numerator and denominator we have
c) 
As 
, the numerator goes to 1 while the denominator goes to zero from above,
so the limit is 
. Put another way, if
x is slightly bigger than 1 (say 1.001), then
the numerator is close to 1 while the denominator is a small possitive
number (like .001), so the ratio is a large positive number (like 1000).
d) 
As 
, the numerator goes to 6, but the denominator goes to zero. If x
is slightly bigger than 4, then the denominator is a small positive number
and the ratio is a large positive number. That is, 
. But if x is slightly less than 4, then the denominator is a small
negative number and the ratio is a large negative number. That is, 
. Since the limits from the two sides do not agree, there is no overall
limit. The correct answer is ``DNE''.
4. Take the derivatives of the following functions with respect to x. You do not need to simplify your answers:
a) 
Use the chain rule: 
.
b) 
Use the product rule: 
.
c) 
You can either use the quotient rule or the chain rule. Since 
, 
.
d) 
Use the quotient rule.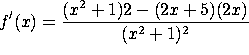 
.
5. New England Widget Technologies (NEWT) makes expensive high-tech widgets. Their marketing department has determined that the demand function is x = 4000 - 2p, where x is the number of widgets sold and p is the price. Their cost function is C(x)= 200,000 + 1000x.
a) Find the price p(x) and the revenue R(x) as a function of x.
Soln: p(x) = (4000-x)/2 = 2000 - x/2. 
.
b) Compute the marginal cost, marginal revenue and marginal profit as a function of x.
Soln: Marginal cost = C'(x) = 1000. Marginal revenue = R'(x)=2000-x. Marginal profit = P'(x) = R'(x)-C'(x) = 1000 - x.
c) The company has a current production level of x=1500. To increase revenue, should the company increase or decrease production? [Note: you do not need to compute the optimal level of production. You just need to say whether it is higher or lower than 1500.]
Soln: Since R'(1500)=2000-1500=500, each additional widget produced will increase revenue by $500. So to increase revenue the company should increase production.
c) The company has a current production level of x=1500. To increase profit, should the company increase or decrease production?
Soln: Since P'(1500)=1000-1500=-500, each additional widget made
will
decrease profits by $500. This makes sense, because each additional
widget costs $1000 to make and only brings in $500 in revenue. So, to increase
profit, the company should decrease production.
