.
This exam consists of 2 parts. Part I contains 10 short ``grab-bag'' questions, each worth 4 points. Part II contains 5 longer problems, each worth 12 points. The exam was closed-book, but allowed a crib sheet. Unlike this year, a non-graphics calculator was allowed.
Evaluate the following derivatives, integrals, and limits, and simplify the following expressions involving exponentials and logs.
For problems A-D, you do NOT have to reduce your answers to the simplest possible forms. Any correct answers will do.
However, for problems E-J, I do want answers in the simplest possible form. For example, if the answer is zero, then writing ``ln(1)'' (which DOES equal zero, of course) will only get you partial credit. Also, you should show your reasoning. Just pulling numbers from a calculator will get you NO credit.
Some of the limits may not exist. If they don't exist, write ``DNE'' or ``does not exist'' in the box.
A. Find f'(x), where
.
Use the product rule. 
B. Evaluate: 
.
.
C. Find f'(x), where 
Product rule again: 
.
D. Find f'(x), where 
and 
.
Chain rule. 
.
E. Evaluate (and simplify): 
Integrate by substitution with 
. 
. Evaluating at x=2 and x=0 gives 
.
F. Evaluate (and simplify): 
By L'Hopital's rule, this equals 
.
G. Evaluate (and simplify): 
By L'Hopital's rule, this gives 
.
H. Simplify: 
, so 
.
I. Simplify: 
.
J. Find dy/dx at the point (2,3), where y is given
by 
. (Your answer should be a NUMBER, not something like 
.)
, so 
.
This part consists of 5 longer problems, each worth 12 points.
Problem 1. A driver goes out on a 4-hour car trip. v(t), his velocity at time t, is given by the formula:
Here t is measured in hours, and v is measured in miles/hour.
Note that parts (a) and (b) below can be done independently of each other. Part (a) involves differentiation, while part (b) involves integration.
a) At what time is the driver driving the fastest? How fast is he going at that time?
To find the critical points, take the derivative and set it equal to zero: 0 = v'(t) = 30 - 15 t, so t=2. By the second derivative test, this is a local max. It is also a global max. So he is going fastest at t=2 and his speed at that time is v(2) = 40 + 60 - 30 = 70.
b) How far does the driver travel in 4 hours?
miles.
Problem 2. Consider the function 
.
a) Find all the local maxima of f(x), all the local minima, and all the points of inflection.
, so the critical points are at x=-1, x=0 and x=+1. 
, so f''(-1);SPMgt;0, f''(0);SPMlt;0 and f''(1);SPMgt;0.
Therefore -1 and 1 are local minima, while 0 is a local maximum. The points
of inflection are where f''(x)=0, namely at 
.
b) For what values of x is f increasing?
For -1 < x < 0 and for x > 1.
c) For what values of x is the graph of f concave up?
For 
and for 
.
Problem 3. C-14, an isotope of carbon, is radioactive. Suppose the radiation from a sample of C-14 decreases at a rate of 0.014% per year, compounded continuously (this figure is pretty accurate).
a) What is the half-life of C-14 (in other words, how long do you have to wait for half the radioactivity to be gone)?
Half life = 
years.
b) If 1 pound of C-14 were deposited 2000 years ago, how much of it would be left today?
c) If a sample of ancient wood contains only one tenth of the C-14 that it used to, how old is it?
, so 
, so 
, so 
16,500 years.
4. a) Use differentials to estimate 
.
, x=10, dx=0.01, 
. 
.
b) The radius of a ball is increasing at a rate of 1 ft/sec. At what
rate is the volume increasing when the radius reaches 10 feet? (Hint: the
volume of a sphere of radius r is given by 
).
cubic feet/second.
5. Consider the function
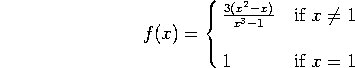
a) Does 
exist? Why or why not? If it exists, what does it equal?
By L'Hopital's rule, the limit is 
.
b) Is f(x) continuous at x=1? Why or why not?
Since the limit equals the value of the function, the function is continuous
at x=1.