1. Evaluate the following limits and improper integrals, or write ``DNE'' if the limit does not exist. EXPLAIN YOUR REASONING.
, which diverges as 
, so the answer is DNE.
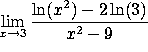
Since 
, this is a 0/0 indeterminate form. By L'Hôpital's rule, the limit
is 
.
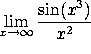
The numerator is bounded while the denominator goes to 
, so the limit is zero.
.
Note that 
, and 
, which goes to zero.
2. Indicate which of these series converge absolutely, which converge conditionally, and which diverge. EXPLAIN YOUR REASONING.
a)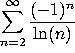 
This is an alternating series that converges. However, 
diverges by comparison to 
, so the answer is CONVERGES CONDITIONALLY.
b)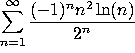 
This CONVERGES ABSOLUTELY by the ratio test (or by the root test).
c)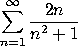 
This DIVERGES by the integral test (compare to problem 1a).
d)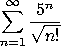 
This CONVERGES ABSOLUTELY by the ratio (or root) test.
3. Consider the infinite power series 
.
a) Find the radius of convergence.
By the root test, the radius of convergence is 
.
b) Use the series to estimate f(0.2). Your answer should be good to 3 decimal places.
.
c) Estimate 
to 3 decimal places.
Two terms are enough: 
.
d) Estimate f'(0.1) to 3 decimal places.
4. Let L be the line through the points (0,1,2) and (3,2,3). Let P be the plane containing the origin and the line L. Let Q=(5,1,2).
a) Find the equation for the line L.
d = (3,2,2)-(0,1,2) = (3,1,1), so our line is 
.
b) Find the equation for the plane P.
We want the plane through (0,0,0), (0,1,2) and (3,2,3). The normal vector
is 
, so the plane is -x + 6y - 3z=0.
c) Find the distance from Q to L.
d) Find the distance from Q to P.
5. Consider the parametrized curve 
a) Find the velocity (vector) at time t=0.
, so 
.
b) Find the speed as a function of time.
The speed is 
.
c) Find the distance traveled (i.e., arclength) from t=-1 to t=1.
Distance = 
speed 
.
6. a) The width of a rectangle is increasing at a rate of 0.2 meters/second, while the height is increasing at a rate of 1 meter/second. At what rate is the area increasing when the height is 10 meters and the width is 0.5 meters?
A = wh, where A is area, w is width and h is height. 
square meters per second.
b) A bird is flying through a forest fire at 6 meters/second, in the
direction (2,2,1). The temperature as a function of position is 
. At what rate is the temperature changing when the bird passes the point
(5,20,10)?
Velocity is a multiple of (2,2,1), so v=k(2,2,1) for some
constant k. Since 
, we have k=2, so v=(4,4,2).
7. Consider the surface 
.
a) Find the equation of the plane tangent to this surface at the point (1,1,1).
The normal vector is 
, so our plane is 2x+2y+5z=9.
b) Find the equation of the line normal to this surface at the point (1,1,1).
Since d=(2,2,5), our line is 
.
8. Consider the function of two variables: 
.
a) Find all critical points of this function.
and 
. Setting these equal to zero gives x=y=0. This is the only
critical point.
b) Use the second derivative test to determine which critical points are local maxima, which are local minima, and which are saddle points.
, 
, and 
, so we are at a local MINIMUM.
9. Find the maximum and minimum values of the function 
on the unit sphere 
. Where do these maximum and minimum values occur?
and 
, so our equations are
The solutions are 
, (-1, 0, 0, 1), 
, 
, 
, and 
. The first two have f=1, the next two have f=2, and the
last two have f=-2, so the last two are minima, the middle two are
maxima, and the first two are neither. That is, the maximum value is 2,
and is achieved at 
, while the minimum value is 2, and is achieved at 
.
10. Let T be the triangle in the x-y plane with
vertices (0,0), (2,0) and (1,1). We are interested in the double integral 
.
a) Write
as an iterated integral, where you integrate first over x and then
over y. (Do not evaluate yet)
b) Break T up into two smaller triangles, 
with vertices at (0,0), (1,0) and (1,1), and 
with vertices at (1,0), (2,0) and (1,1). Write 
as an iterated integral, where you integrate first over y and then
over x. Do the same for 
.
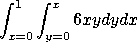and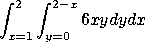 
.
c) Compute
, either by doing the iterated integral you wrote down in (a) or the ones
you wrote down in (b).
In (a), 
, so our outer integral is 
.