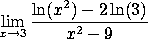
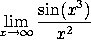
M408D Final Exam, December 14, 2002
1. Evaluate the following limits and improper integrals, or write
``DNE'' if the limit does not exist. EXPLAIN YOUR REASONING.
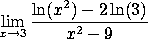
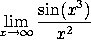
2. Indicate which of these series converge absolutely, which converge conditionally, and which diverge. EXPLAIN YOUR REASONING.
a)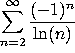 
b)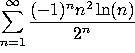 
c)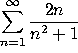 
d)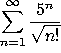 
3. Consider the infinite power series 
.
a) Find the radius of convergence.
b) Use the series to estimate f(0.2). Your answer should be good to 3 decimal places.
c) Estimate 
to 3 decimal places.
d) Estimate f'(0.1) to 3 decimal places.
4. Let L be the line through the points (0,1,2) and (3,2,3). Let P be the plane containing the origin and the line L. Let Q=(5,1,2).
a) Find the equation for the line L.
b) Find the equation for the plane P.
c) Find the distance from Q to L.
d) Find the distance from Q to P.
5. Consider the parametrized curve 
a) Find the velocity (vector) at time t=0.
b) Find the speed as a function of time.
c) Find the distance traveled (i.e., arclength) from t=-1 to t=1.
6. a) The width of a rectangle is increasing at a rate of 0.2 meters/second, while the height is increasing at a rate of 1 meter/second. At what rate is the area increasing when the height is 10 meters and the width is 0.5 meters?
b) A bird is flying through a forest fire at 6 meters/second, in the
direction (2,2,1). The temperature as a function of position is 
. At what rate is the temperature changing when the bird passes the point
(5,20,10)?
7. Consider the surface 
.
a) Find the equation of the plane tangent to this surface at the point (1,1,1).
b) Find the equation of the line normal to this surface at the point (1,1,1).
8. Consider the function of two variables: 
.
a) Find all critical points of this function.
b) Use the second derivative test to determine which critical points are local maxima, which are local minima, and which are saddle points.
9. Find the maximum and minimum values of the function 
on the unit sphere 
. Where do these maximum and minimum values occur?
10. Let T be the triangle in the x-y plane with
vertices (0,0), (2,0) and (1,1). We are interested in the double integral 
.
a) Write
as an iterated integral, where you integrate first over x and then
over y. (Do not evaluate yet)
b) Break T up into two smaller triangles, 
with vertices at (0,0), (1,0) and (1,1), and 
with vertices at (1,0), (2,0) and (1,1). Write 
as an iterated integral, where you integrate first over y and then
over x. Do the same for 
.
c) Compute
, either by doing the iterated integral you wrote down in (a) or the ones
you wrote down in (b).