} is said to ``grow faster'' than { 
} if 
. Put the following sequences in order of growth rate, from fastest to
slowest. Justify your answers.
1. A sequence {
} is said to ``grow faster'' than {
} if
. Put the following sequences in order of growth rate, from fastest to
slowest. Justify your answers.
Note that 
and that 
. The sequence 
(factorial) grows faster than
(exponential), which grows faster than 
(power), which grows faster than 
(smaller power), which grows faster than
(log).
2. Evaluate the following limits or improper integrals, or write DNE if the limits do not exist.
a)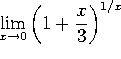 
. If you let n=1/x, this is 
.
b) 
. Since 
(integrate by parts), we have 
, which goes to 1 as 
.
c)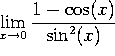 
. This is a ``0/0'' indeterminate form. Applying L'Hopital's rule once
gives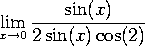 
, which equals 1/2.
d)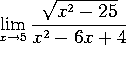 
. This is NOT an indeterminate form. It is 0/(-1)=0.
3. Which of the following series and integrals converge, and which diverge.
In each case, give a 1-sentence explanation (e.g., ``converges by ratio
test'', or ``diverges by comparison to 
'')
a)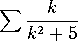 
diverges by integral test, or by comparison to 1/2k.
b)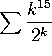 
converges by ratio test or by root test.
c) 
diverges. Terms don't go to zero.
d)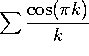 
. This is a funny way of writing the alternating series 
, which converges.
4. a) Write down the Taylor series for 
.
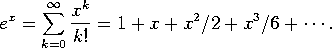
b) Write down the 6-th order Taylor polynomial (i.e., through the 
term) for 
.
, so the answer is 
.
c) Evaluate 
. (That is, the 6-th derivative of
f(x), evaluated at x=0.)
The coefficient of
, namely 8, is the answer divided by 6!, so the answer must be 8(6!) =
8(720) = 5760.
d) Evaluate 
to five decimal places. (No, you don't need a calculator!)
The third-order Taylor polynomial is good enough:
.
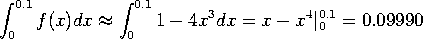5. a) Find the second-order Taylor polynomial for 
around x=4.
, 
and 
. Taking
a=4 we have f(a)=2, f'(a) =
1/4 and f''(a)=-1/32, so
[OOPS! That should be powers of (x-4), not of (x-2).]
b) What is the radius of convergence of the power series 
? Justify your answer.
By the root test, 
, so the radius of convergence is 2. (The ratio test would work just as
well).