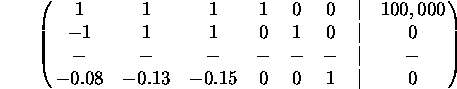Spring '98 403L Final Exam Solutions

1. A population of bacteria is growing exponentially. At noon today there were 1,000. At 2 PM there were 1,500 bacteria.

a) How many bacteria will there be t hours after noon?

b) How many bacteria will there be at noon tomorrow?

c) At what time will there be 10,000 bacteria?

Exponential growth implies for some constant k. Since y(0)=1000 and y(2)=1500, we have , so . So a) . b) Tomorrow at noon there will be bacteria. c) , so , so , so . (TYPO! That should be 11.36, not 5.68) 0.36 hours is 21 minutes, so we will have 10,000 bacteria at 11:21 PM.

2. Consider the function .

a) Which of the following points are critical points: (1,-1), (1,0), (1,1), and (0,0)?

b) Of the above, classify which critical points are local maxima, which are local minima, and which are saddle points.

a) Compute the first partial derivatives. , . Plugging in the different points shows that (0,0) and (1,-1) are critical points and the others aren't.

b) Compute the second partials: , , . At (0,0) we have and , so it's a local min. At (1,-1) we have and , so it's a saddle point.

3. Evaluate the double integral of the function f(x,y)=24xy over the region between the line y=x and the parabola . [Hint: you can slice either vertically or horizontally, but one approach is a bit easier than the other].

Slicing horizontally we have

Slicing vertically we have

4. Consider the function .

a) Find the 2nd order Taylor polynomial for f(x) around x=0.

b) Use this polynomial to approximate f(-0.1).

c) Use this polynomial to approximate .

a) , , so f(0)=1, f'(0)=1 and f''(0)=-1, so our 2nd-order Taylor polynomial is . b) . c) .

5. Use Newton's method to find the point (x,y) where the curves and intersect. Your answer should be correct to at least 5 decimal places.

, . Take initial guess . Then , , so . , , so . , , so . is about , so is close enough. Taking , our point is (0.636039, 1.529385).

6. a) Evaluate exactly.

b) Approximate this integral numerically using Simpson's rule with . Express your result to at least four decimal places.

a) Integrating by parts gives .

b) Evaluate f(1), f(1.5), etc. up to f(3). Then our integral is approximately . Remarkably close!

7. a) A certain baseball player has a 0.300 chance of getting a hit every time he comes to bat. Assuming he bats 500 times this season, write down the exact probability that he has 160 or more hits this season. You can express your answer as a sum - you need not attempt to evaluate the sum numerically.

b) Estimate this probability numerically using the normal distribution (see attached table).

a) This is binomial with p=0.3 and n=500. The exact probability is

.

b) The mean is , the variance is np(1-p)=105, so . Setting , we have , or about a 17.6% chance.

8. Until 1964, dimes (and quarters and half-dollars) were made of silver. There are a few of these old silver coins still in circulation - about one in a thousand dimes is silver. Assuming you handle 5 dimes every day, what is the probability of your encountering 2 or more silver dimes in the next year? (For the record, I was handed a silver dime at Burger King last month, and my daughter found a silver half-dollar on the ground earlier this year.)

This is Poisson with . .

9. A continuous random variable is described by the probability density function

where C is a constant.

a) Find the constant C that makes f(x) into a legal probability density function.

b) Find the probability that 2 < X < 3.

c) Find the mean and standard deviation of X.

a) C=3, so that . b) . c) . . Var= , so .

10. For the system of linear equations:

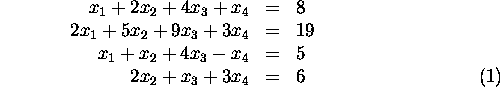
a) Write down the augmented matrix.

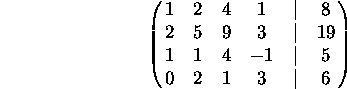
b) Apply row operations to put this matrix in reduced form.

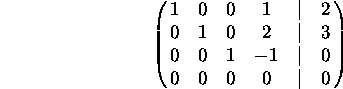
c) Find all solutions to the system of linear equations.

, , , , and t is any real number.

11. Maximize subject to the constraints:

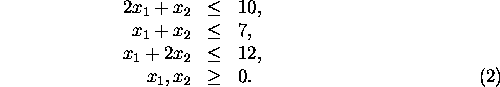
You may recognize this as a practice homework problem. Max P=260 at and .

12. Express the following situation as a linear programming problem. That is, a) set up the inequalities, b) choose slack variables, and c) write down the matrix of the initial system. You do not have to actually solve the resulting system:

``An investor has at most $100,000 to invest in government bonds, mutual funds and money market funds. The average yields for these investments are 8%, 13% and 15%, respectively. To avoid undue risk, the total amount invested in mutual and money market funds cannot exceed the amound invested in government bonds. How should the money be invested to maximize expected return?''

Let , and be the amounts invested in the bonds, mutual funds and money market funds. We want to maximize subject to , and . Define the slack variables and such that and , and we now also have . Our initial matrix is