Fall '98 M403L Final Exam with Solutions

Problem 1. Max-min. (30 pts)

a) Find all critical points of the function f(x,y)=xy-2x-y. Determine which are maxima, which are minima and which are saddle points.

Take partial derivatives and set them equal to zero: , so y=2. , so x=1. Our only critical point is at (1,2). Now apply the 2nd derivative test: , , C=fyy=0. Since , we have a saddle point.

b) Maximize the function f(x,y)=3x-4y on the circle .

. We compute: , so . , so . , so , so .

If , then x=-3, y=4 and f= -25. This is a minimum. If , then x=3, y=-4 and f= 25. This is our desired maximum.

c) Minimize the function on the line 3x-4y=50.

The calculations are quite similar to those in (b). Let . Setting gives . Setting gives . Setting gives , so our maximum is at x=6 and y=-8 (and f=100.)

Problem 2. Double integrals. (20 pts)

a) Sketch the region of integration for the double integral .

This is the region between the parabola and the line y=x+1. The points of intersection are at (0,1) and (1,2). Sorry, but I don't know how to sketch it on the computer!

b) Rewrite the integral as an integral first over x and then over y. That is, ``switch the order of integration''.

y=x+1 means x=y-1, and means , so we have

(OOPS! That should be dx dy, not dy dx. Thanks to Andrew Friedberg for pointing that out.)

c) Evaluate the double integral (in either form - your choice).

Done the first way we have: .

Done the second way we have (Again, should be dx dy, not dy dx).

Either way the answer is 1.

Problem 3. Differential equations (10 pts)

Consider the differential equation .

a) Find the integrating factor I(x).

b) Find the general solution to the differential equation.

.

Problem 4. Limited growth (20 pts)

Recall that heating and cooling is described by the limited growth equation dT/dt = k(M-T). A pizza at room temperature (70 degrees) is placed in a hot oven (400 degrees). After 2 minutes the pizza has reached 120 degrees.

a) Find the values of k and M. (M is essentially given to you; k must be computed).

M=400. Our solution is . Since T(0)=70, we must have C=330, so . Since T(2)=120 we have , so and .

b) What temperature with the pizza be after 5 minutes?

degrees.

c) When will the pizza reach a temperature of 200 degrees?

, so , so .

Problem 5. Taylor series and numerical integration (30 pts)

Consider the function .

a) Find the second-order Taylor polynomial for f(x) around x=1. [NOT around x=0!]

, so f(1)=1. , so f'(1)=3. , so f''(1)=5. Our Taylor polynomial is therefore .

b) Use the result of (a) to approximate .

.

c) Use Simpson's rule with N=4 to approximate . (Use the actual function f(x), not the Taylor polynomial).

f(0.8) = 0.4745, f(0.9)=0.7216, f(1)=1, f(1.1)=1.3290, f(1.2)=1.7350, so

Extra credit (up to 10 points, answer on back): About how accurate do you expect each of the approximations [(b) and (c)] to be? (This is an open-ended question and could easily eat up a lot of time. Do it after you're done with everything else!)

is good to about , which is no more than 0.008. Integrating this over a region of size 0.4 gives an integral accurate to at least 0.003. In fact, it turns out to be even more accurate, because the errors proportional to cancel out, and we only get the ones proportional to and higher order.

Simpson's rule has an error of roughly , so it's good to about 5 or 6 decimal places.

Problem 6. Exponential and Poisson Distributions (40pts).

When Jacques goes fishing at his favorite lake in France, he catches an average of 1.5 fish per hour, distributed according to the Poisson distribution. The time he has to wait between one catch and the next is described by the exponential distribution, with mean 40 minutes. Jacques starts fishing at 6 AM and keeps at it until 6 PM.

[Note: the French word for fish is ``poisson'', which is what motivated this problem]

a) What is the probability that Jacques catches no fish in his first half-hour of fishing?

This is Poisson with mean (1/2)(1.5)=0.75, so the probability of zero is .

b) What is the probability that Jacques catches exactly 2 fish between 8 AM and 9 AM?

This is Poisson with mean 1.5, so .

c) What is the probability that Jacques has to wait 30 minutes or more for his first fish?

The wait is exponential with mean 40 minutes, so the probability of waiting 30 minutes or more is . This is the same answer as (a), which makes sense, since waiting more than 30 minutes for your first fish is the exact same thing as not catching any fish in the first 30 minutes!

d) What is the probability that Jacques' first fish is caught between 6:30 and 7:00?

Again, this is exponential with mean 40 minutes. .

e) Use the normal distribution to approximate the probability that Jacques catches 23 or more fish in his 12 hours of fishing.

This is Poisson with mean and variance , hence standard deviation . Approximating this by a normal distribution we get .

Extra credit (10 pts): Use the normal distribution to approximate the probability that Jacques' 9th fish is caught between noon and 1 PM.

The time to wait for nine fish is the sum of nine identical random variables, namely the time spent waiting for each of the nine fish. It is therefore a random variable with mean 9 times bigger and standard deviation 3 times bigger than the wait for the first fish. That first wait is exponential, so it has minutes. So our sum time has minutes, that is 6 hours, and a standard deviation of 120 minutes, or 2 hours. Using the normal approximation, we have P(6 < X < 7) = P(0 < Z < 1/2) = 0.1915.

Problem 7. Continuous probability (10 pts) Let X be a continuous random variable with pdf

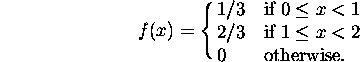
Find the cdf F(x) for all values of x.

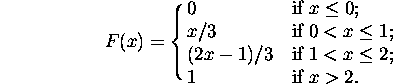
Problem 8. Linear programming. (20 points) Set up the following problem, that is: a) Define your variables, b) write down the objective function and the constraints, c) define slack variables, and d) write down the initial matrix. YOU DO NOT HAVE TO ACTUALLY SOLVE THE PROBLEM:

``A department store chain has up to $20,000 to spend on television advertising. An ad on daytime TV costs $1,000 and reaches 14,000 people. A prime-time ad costs $2,000 and reaches 24,000 customers. A late-night ad costs $1,500 and reaches 18,000 customers. The TV station will not accept more than 15 ads, total. How many ads of each type should the store run to maximize the number of customers reached?''

a) Let be the number of daytime ads, the number of prime time ads, and the number of late night ads.

b) Our objective is . The constraints are and .

c) Set , .

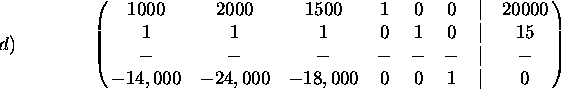
Problem 9. Simplex method. (20 points) The following matrix describes a partially completed linear programming problem.

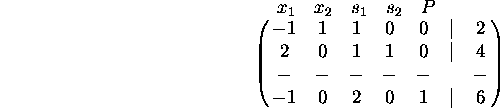
a) What are the basic variables and what are the non-basic variables?

, and P are basic, while and are nonbasic.

b) What are the values of all the variables at the point described by this matrix?

, so , and P=6.

c) Apply ONE iteration of the simplex method to get a new matrix. Is the answer you get optimal? (In other words, is the problem finished, or are more iterations needed?)

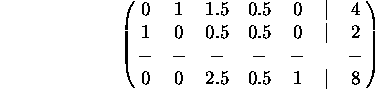
This is optimal, as the bottom row is all non-negative. The optimal solution is , , and P=8.