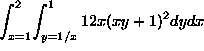M403L Second Midterm Solutions

Warning: There are some glitches in converting TeX to HTML

Problem 1. Evaluate the iterated integral .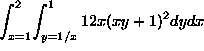

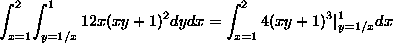
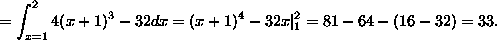
Problem 2. Consider (but do not evaluate!) the iterated integral .

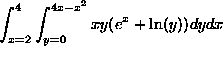a) Sketch the region of integration.

This is the region between the x axis and the parabola to the right of the line x=2. The three ``corners'' are (2,0), (2,4) and (4,0).

b) Rewrite the expression as an integral dx dy (That is, ``switch the order of integration''). You do NOT have to evaluate this integral, just write it down. [You may find it convenient to rewrite 4x-x^2 as .]

If y=4x-x^2, then , so our answer is

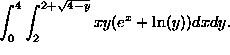
Problem 3. Consider the differential equation , whose general solution is .

a) Find the particular solution with y(0)=2.

, so 4=1+C, so C=3: .

b) If y(0)=2, what is the value of y(3)?

.

Problem 4. Consider the differential equation .

a) Find the integrating factor I(x). [Simplify your answer as much as possible]

.

b) Find the general solution to the differential equation. [Again, you should simplify your answer as much as possible].

Problem 5. A certain pollutant is emitted at a rate of 1,000 tons per year. It is broken down in the environment at a rate of 10% (of the amount out there) per year.

a) Write down the differential equation that describes this situation. [You do not have to solve the differential equation].

Let y be the amount of pollutant. Then dy/dt = 1,000 - 0.1 y = 0.1(10,000 - y).

b) Is this equation of a type you (should) recognize? Describe qualitatively what happens over time.

It's a limited growth equation, so y approaches its limiting value exponentially. The actual solution (which you didn't need to get) is .

Problem 6. a) Find the second-order Taylor polynomial that approximates the function near x=8.

, f(8)=16, ; f'(8)=8/3, ; f''(8)=1/9. .

b) Use this polynomial to approximate .

. In fact, is about 13.391.