Problem 1. Cheating
In large, lower-division classes, 90% of professors apply a ``watch them like a hawk'' policy to prevent cheating, while 10% rely on an honor code. Cheating on exams is a serious problem in 20% of the classes with an honor code, and in 30% of the classes without an honor code.
a) What is the probability of a randomly chosen class having a Serious Cheating Problem?
Let A be the event ``Uses honor code'', and let B be ``has cheating
problem''. Then
b) If a class does have a Serious Cheating Problem, what is the probability that the class is being run on an honor code?
P(A|B)=P(B|A)P(A)/P(B)=0.02/0.29 = 2/29.
[Note: the numbers in this problem are made up, and reflect my own perception of reality. I strongly believe in honor codes, but I'm not so naive as to believe that everybody is honest. Rather, I believe that a) honest students have a right to be treated with dignity and trust, and b) the best way to make somebody trustworthy is to trust him.]
Problem 2. Big Six
In the game of Big Six, a player rolls four dice. If three or more of the dice show a 6, the player wins.
a) Compute the probability of winning.
This is binomial with p=1/6 and n=4. P(3 sixes)= 
, while P(4 sixes)= 
, so P(winning)= 
=7/432.
b) A person plays the game 216 times. Let X be the number of times he wins. What type of random variable is X?
Strictly speaking this is a binomial random variable (with n=216
and p=7/432). However, it is extremely well approximated by a Poisson
random variable (with 
). I'll accept either answer.
c) Find the expectation of X.
E(X)=np=3.5.
Problem 3. Manipulating pdfs
A continuous random variable X has pdf:
a) Compute the cdf 
for all values of x (not just between 0 and 2.)
Just integrate the fdf:
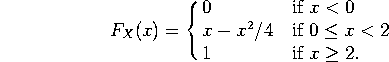
b) Compute the probability that X <1/2.
c) Find the mean and variance of X.
Problem 4. A knotty problem
The number of knots in a piece of lumber is described by a Poisson distribution, with an average of 0.08 knots per square foot.
a) What is the probability that a 10 square foot piece of lumber has zero knots in it?
Poisson with 
: 
.
b) I buy a 10 square foot piece and a 15 square foot piece. What is the probability that I wind up with exactly 3 knots. (Simplify as much as possible).
Since 10+15=25, this is Poisson with 
. 
. The fact that my 25 square feet of lumber is in two pieces is irrelevant
(compare with problem 5c from the 1991 exam).
c) If I purchase 1250 square feet of lumber, estimate the probability of my getting 85 or fewer knots.
Poisson with mean 
and standard deviation 
. So 
.
Some people wrote that the variance was npq, with p=0.08, as if this
were binomial. This is NOT a Poisson approximation to a binomial
distribution. It is a Poisson distribution, period.
Problem 5. Summer heat
The high temperature for a day can be described by a normal distribution with a certain mean and standard deviation. For July 10, the average high is 94.5 degress, and the standard deviation is 6.0 degrees. For July 23, the average high is 95.4 degrees and the standard deviation is 8.0 degrees.
a) What is the probability that the high on July 10 will be under 90.1 degrees.
90.1 degrees is 4.4/6=0.733 standard deviations below average, so 
.
b) What is the probability that the high on July 23 will be over 100.0 degress.
100 degrees is 4.6/8=0.575 standard deviations above average.
P(X > 100) = P(Z > 0.575) = 1 - F(0.575) = 1 - 0.7173 = 0.2827.
c) What is the probability that the high on July 23 will be hotter than the high on July 10? You may assume that the temperature on July 23 is independent of the temperature on July 10.
This was probably the most difficult problem on the test, in that it's
not just follow-your-nose. Let X be the temperature on July
23 and let Y be the temperature on July 10. X-Y is
a normal random variable with mean 0.9 and standard deviation 
. We are interested in the probability that X-Y is positive. Having
X-Y=0 means having X-Y be 0.09 standard deviations below
average, so 
.
Problem 6. The Senate
The United States Senate has 100 members, two from each state. Currently, 87 are men and 13 are women. A committee of 50 is chosen at random from among the 100 US Senators.
a) What is the probability that the committee will have 43 men and 7 women?
The number of ways to choose 43 men is 
and the number of ways to choose 7 women is 
, while the number of ways to choose 50 senators is 
, so the probability of choosing 43 men and 7 women is 
.
b) What is the probability that each state will be represented on the committee? (Note: Each state has exactly two senators).
There are 
ways to choose a senator from each state, so the answer is 
.
Problem 7. Sample Spaces
Two positive numbers, X and Y, are picked so that X is less than Y, and so that the sum of X and Y is less than 4.
a) Draw a picture of the sample space S.
A point in the sample space is an ordered pair (X,Y), so S is a subset of the plane. Specifically,
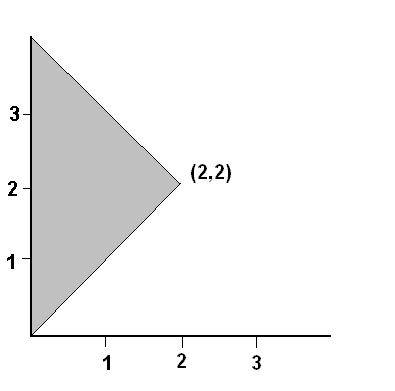
S is a triangle bounded by the Y-axis, the line X=Y, and the line X+Y=4.
The vertices of the triangle are at (0,0), (2,2) and (0,4). Note
that the total area is 4.
b) Draw a picture of the event ``Y < 3''.
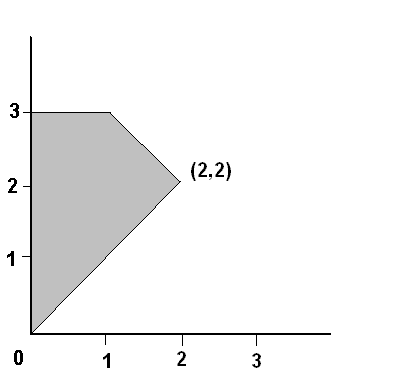
Note that events are SUBSETS of the sample space. That is, we want all the points (X,Y) in the sample space that satisfy the extra condition Y<3. This is pictured above.
c) Suppose the joint probability is uniform (that is, the probability of a subset of S is proportional to its area). Compute the probability that Y < 3.
The area left out is 1/2, so the area of this event is 7/2, and the
probability is 7/8.