Note that this test was given about 2 weeks farther into the term than we are now. As a result, some of the questions are about Chapter 3 material, and you shouldn't expect to be able to do them yet.
Problem 1. Teddy Bears
My daughter Rina has lost her favorite teddy bear. From past experience, I estimate that there is a 2/3 chance it is in her room somewhere, and a 1/3 chance that it is in her brother's room. If the bear is in her room and she looks hard, she has a 3/5 chance of finding it. I tell her to go back to her room and look hard.
a) What is the probability of her finding the bear?
Let A be the event that the bear is in her room, and let B be the event that she finds it. P(A)=2/3, P(B|A)=3/5, and P(B|not A)=0, so P(B)=P(A)P(B|A)+ P(not A)P(B|not A)=(2/3)(3/5)+0 = 2/5.
b) Let's suppose Rina comes out of her room a few minutes later, still missing her bear. What is the probability that the bear is in her brother's room, given that she failed to find it in her room?
![]() .
.
Problem 2. The Texas Lottery
In the ``Pick Six'' game in the Texas Lottery, you pick 6 numbers between 1 and 40, the state picks 6 numbers, and if 3 of your numbers match you win ``an average of $ 25''. (If you match more than 3 you win more money, but in this problem we'll just talk about the odds of matching 3). [Disclaimer: All I know about the lottery is what I see in the TV ads. I may well have misrepresented the ``Pick Six'' game. If so, just pretend that the game is played by my rules.]
a) Each time you play Pick Six, what is the probability of your matching exactly 3 of the winning numbers? (You can leave your answer in terms of factorials or binomial coefficients).
The total number of possible drawings is ![]() . The number of ways to match 3 of your 6 (and 3 of the remaining 34) is
. The number of ways to match 3 of your 6 (and 3 of the remaining 34) is ![]() . So the answer is
. So the answer is ![]() .
.
OOPS!! THERE'S A TYPO. WHEREVER YOU SEE "34 choose 6" IT REALLY SHOULD BE "34 choose 3". SORRY!!
b) Suppose you play the numbers 1-2-3-4-5-6 and a friend plays 7-8-9-10-11-12. What is the probability that at least one of you matches (exactly) 3 of the winning numbers?
Let A be the event that you match 3 and let B be the event that your
friend matches 3. P( ![]() )=P(A)+P(B) - P(
)=P(A)+P(B) - P( ![]() ) =
) =
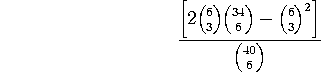
AGAIN, "34 CHOOSE 6" SHOULD BE "34 CHOOSE 3".
Problem 3. Continuous distributions
Suppose I pick a number x at random (i.e. by the uniform distribution) between 0 and 2. Suppose I pick y at random between 0 and 4.
a) Describe the sample space. Draw a picture of the sample space. In
your picture, show the event `` ![]() ''.
''.
The picture should be the rectangle with corners (0,0), (2,0), (2,4)
and (0,4). The event ![]() is everything under the parabola
is everything under the parabola ![]() .
.
b) Find the probability that ![]() .
.
The area of the event is ![]() . The area of the total region is 8, so the probability of the event is
(8/3)/8 = 1/3.
. The area of the total region is 8, so the probability of the event is
(8/3)/8 = 1/3.
Problem 4. Breakdowns
A system consists of 4 components (call them A, B, C, and D). On a given day, each component has a probability p of failing (independent of the others). If 3 or more components fail, the system breaks down.
a) What is the probability of the system breaking down today? (Leave your answer in terms of p, but otherwise simplify as much as possible).
P(breakdown) = P(3 failures) + P(4 failures) = ![]() .
.
b) Given that the system broke down yesterday, what is the probability that component A failed?
The only scenario that doesn't involve A failing is if B, C, and D fail
and A doesn't. This has probability ![]() . The remaining scenarios have probability
. The remaining scenarios have probability ![]() . So the conditional probability is
. So the conditional probability is
P(A failed| breakdown) = 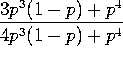 .
.