; 
; 
; 
; 
; 
; 
; 
; 
. a) Compute the marginal probability densities 
and 
. b) Are the variables X and
Y independent? c) What is the
(conditional) probability that X=2 given that Y=1? d) Are
the events X=1 and Y=0 independent?
Note: This is for practice only. The actual exam will not cover
random variables (problems 4 and 5). For extra practice on combinatorics,
look at the practice first exams. You may want to save problems 4 and 5
to help you practice for the third exam.
Problem 1: A baseball team needs to win 4 (or more) of their last 6 games to win the pennant. Assuming they're a good team team, and have a 60% chance of winning any given game, what is the probability of their winning the pennant?
Problem 2: There are 5 blue balls, 3 red balls and one white ball in an urn.
a) If you pick 4 balls without replacement, what is the probability of drawing (exactly) 2 blue balls?
b) If you draw 4 balls WITH replacement, what is the probability of drawing (exactly) 2 blue balls?
Problem 3: A standard bridge hand consists of 13 cards. a) What is the probability of being dealt a hand with exactly 4 spades, 4 hearts and 4 diamonds (and one club)? b) What is the probability of being dealt 4 spades OR 4 hearts OR 4 diamonds? (For both parts, write down an exact expression but do not attempt to simplity).
Problem 4: X and Y are discrete random variables. Their
joint probability density function is:
;
;
;
;
;
;
;
;
. a) Compute the marginal probability densities
and
. b) Are the variables X and
Y independent? c) What is the
(conditional) probability that X=2 given that Y=1? d) Are
the events X=1 and Y=0 independent?
Problem 5: a) X and Y are continuous random variables
with the joint density function 
if 0 < y < x and 0 otherwise. Compute the density function 
and the probability that X < 0.4. b) Let Z be a continuous
random variable with density function 
for z > 1. Compute the cumulative distribution function 
and the mean E(Z).
Problem 1: The number of games won is given by a binomial distribution
with n=6 and p=0.6. We care about k=4,5,6. The answer
is 
Problem 2a. This is hypergeometric. There are 5 blue balls and 4 non-blue
balls, so the answer is 
. You can also get the same answer by adding the probability of (2 blue,
1 white, 1 red) to the probability of (2 blue, 2 red).
Problem 2b. This is binomial. 
.
Problem 3a. You must choose 4 of the 13 spades, 4 of the 13 hearts,
4 of the 13 diamonds, and 1 of the 13 clubs. The number of ways of doing
this is 
. Dividing by the number of hands, 
, we get our answer.
Problem 3b. By the inclusion/exclusion principle, P(4S OR 4H OR 4D) = P(4S)+ P(4H) + P(4D) - P(4S AND 4H) - P(4S AND 4D) - P(4H AND 4D) + P(4S AND 4H AND 4D) = 3P(4S) - 3P(4S AND 4H) + P(4S AND 4H AND 4D), which totals
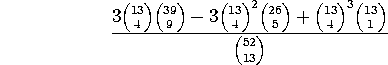
Problem 4. a. Adding rows and columns we get 
, 
, 
, 
, 
, 
.
b. No. Since 
, (one of many possible examples), X and Y are not independent.
c. 
.
d. Since 
, the two events ARE independent.
Problem 5a. 
. 
.
5b. 
. 
.