).
(Solutions below.)
Problem 1. Monday Blues
A word is chosen at random from the (undoubtedly true) sentence ``I hate to take math tests on Mondays''. That is, each word has an equal chance of being chosen. Let X be the number of letters in the word. Let Y be the number of vowels in the word (yes, the ``y'' in Mondays counts as a vowel).
a) Write down the pdf of X (that is,
).
b) Compute the expectation E(X).
c) Write down the joint pdf 
.
d) Are the events X=4 and Y=2 independent? Are the events X=6 and Y=2 independent? Are X and Y independent random variables?
Problem 2. Joint distributions
Let X and Y be independent continuous random variables, each chosen uniformly in the interval [0,1]. That is,
Let Z be the larger of X and Y. That is,
a) What is the probability that ( 
and 
)?
b) Compute the cumulative distribution function 
.
c) Compute the probability density function 
.
d) Compute the expectation E(Z).
Problem 3. Reading CDFs
A random variable X has cumulative distribution function
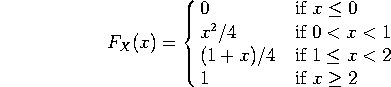
(You may find it helpful to sketch this function).
a) What is the probability that X=0? What is the probability that X=1? What is the probability that X=2?
b) What is the probability that 
?
c) What is the probability that 
?
d) What is the probability that X > 1.5
Problem 4. Manipulating random variables
Let X be continuously distributed between 1 and e with pdf
a) Compute E(X).
b) Compute 
.
c) Let 
. Compute 
, and from it compute 
.
d) Compute E(Y). [There are two ways to do this. One uses
the results of part (b). The other does not.]
SOLUTIONS
Problem 1. Monday Blues
A word is chosen at random from the (undoubtedly true) sentence ``I hate to take math tests on Mondays''. That is, each word has an equal chance of being chosen. Let X be the number of letters in the word. Let Y be the number of vowels in the word (yes, the ``y'' in Mondays counts as a vowel).
a) Write down the pdf of X (that is,
).
There are 8 words in all, one with one letter and one vowel (I) , two with two letters and one vowel (to, on), one with four letters and one vowel (math), two with four letters and two vowels (hate, take), one with 5 letters and one vowel (tests) and one with 7 letters and 3 vowels (Mondays). Since each word has an equal probability, the joint pdf is given in the following table:
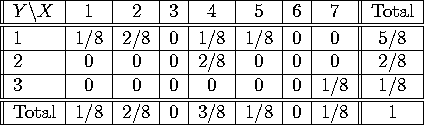
The marginal pdf for X can be read off the bottom.
b) Compute the expectation E(X).
.
c) Write down the joint pdf
.
(see above)
d) Are the events X=4 and Y=2 independent? Are the events X=6 and Y=2 independent? Are X and Y independent random variables?
P(X=4 and Y=2)=2/8, while P(X=4)=3/8 and P(Y=2)=2/8. Since 2/8 is not equal to 3/8 times 2/8, the events X=4 and Y=2 are not independent.
P(X=6)=0, P(Y=2)=2/8, and P(X=6 and Y=2)=0, which does equal 0 times 2/8, so these events ARE independent.
Since X=4 and Y=2 are not independent events, X and Y are not independent random variables.
Problem 2. Joint distributions
Let X and Y be independent continuous random variables, each chosen uniformly in the interval [0,1]. That is,
Let Z be the larger of X and Y. That is,
a) What is the probability that (
and
)?
Since X and Y are independent, P(X < 1/2 and Y <
1/2)=P(X < 1/2) P(Y < 1/2) = P 
= 
= 1/4. (I suppose one should say "less than or equal to 1/2", rather
than "< 1/2", but for a continuous distribution it doesn't matter).
b) Compute the cumulative distribution function
.
Since Z is the larger of X and Y,
and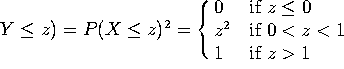 
c) Compute the probability density function
.
d) Compute the expectation E(Z).
.
Problem 3. Reading CDFs
A random variable X has cumulative distribution function
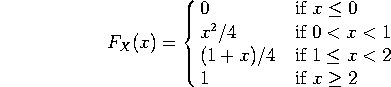
(You may find it helpful to sketch this function).
a) What is the probability that X=0? What is the probability that X=1? What is the probability that X=2?
P(X=0) = (jump in
at x=0) = 0.
P(X=1) = (jump in
at x=1) = 1/4.
P(X=2) = (jump in
at x=2) = 1/4.
b) What is the probability that
?
P(
) = 
.
c) What is the probability that
?
This is the same as (b), plus the probability that X=1/2 (which is zero), minus the probability that X=1 (which is 1/4), that is 7/16 + 0 - 1/4 = 3/16.
d) What is the probability that X >1.5
This is 
.
Problem 4. Manipulating random variables
Let X be continuously distributed between 1 and e with pdf
a) Compute E(X).
b) Compute
.
This is zero if 
and one if 
. If 1 < x < e, then 
.
c) Let
. Compute
, and from it compute
.
.
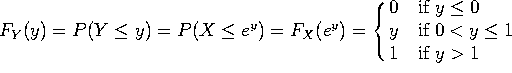In other words, Y is uniformly distributed between 0 and 1.
d) Compute E(Y). [There are two ways to do this. One uses the results of part (b). The other does not.]
, or
.