Problem 1. Final Exams
The final exam for a certain math class is graded pass/fail. A randomly chosen student from a probability class has a 40% chance of knowing the material well. If he knows the material well, he has an 80% chance of passing the final. If he doesn't know the material well, he has a 40% chance of passing the final anyway.
a) What is the probability of a randomly chosen student passing the final exam?
Let A be the event ``knows material'' and B be ``passes exam''.
b) If a student passes, what is the probability that he knows the material?
Problem 2. Hot Pickups
There are 123,850 pickup trucks in Austin. Of these, 2,477 are stolen. [OK, I'm making these numbers up.] Suppose that 100 randomly chosen pickups are checked by the police.
a) What is the probability that exactly 3 of the 100 chosen pickups are stolen. Give an EXACT answer, but do not evaluate it numerically.
This is hypergeometric:
b) Approximate this using the binomial distribution. What are n and p?
n=100, p=2,477/123,850=0.02, so the answer is 
.
c) Approximate your answer to (b) using the Poisson distribution. What
is 
?
, so the answer is 
.
Problem 3. Four Flushers
a) In poker, a ``four-flush'' is a hand with 4 cards of one suit, and one card of another suit. (This sort of hand isn't worth anything, and can be very frustrating). Find the probability of a (5-card) hand being a four-flush.
There are 4 ways to choose the main suit, 
ways to choose the cards from that suit, 3 ways to choose the other suit
and 13 ways to choose the card from that other suit. Dividing by the number
of possible hands, we get
b) A ``three-flush'' is a hand with 3 cards of one suit, one of another suit and one of a third suit. (For instance, 3 spades, one heart and one club. A hand with 3 spades and 2 diamonds would not count.) Find the probability of a three-flush.
There are 4 ways to choose the main suit, 
ways to choose the cards of that suit, 
ways to choose the other two suits, and 
ways to choose those last two cards.
Problem 4. Joint distributions (2 pages)
X and Y are continuous random variables with joint pdf
a) Let Z=X+Y Find the pdf of Z.
If z is between 0 and 2, then we integrate 1/2 from x=0 to x=z to get z/2. Otherwise we get nothing:
b) Find the pdf of X (that is, 
) and that of Y.
To get 
integrate over y from y=0 to y=2-x, so
. The computation for 
is essentially the same: 
.
c) Find the expectation and variance of X.
.
.
.
d) Find the covariance Cov(X,Y).
, so 
.
Problem 5. Quidditch
A game of Quidditch lasts until a player catches the Golden Snitch, which can happen at any time. Meanwhile, both teams try to score goals. The scoring by the two teams is described by independent Poisson processes. The Gryffindor team scores an average of 2.4 goals per hour, while the Slytherin team scores an average of 2.0 goals per hour.
A certain match between Gryffindor and Slytherin lasts 20 hours.
a) What is the probability that Slytherin doesn't score in the first half hour?
Let S be the number of Slytherin goals. This is Poisson with 
(2.0 per hour times half an hour), so 
.
b) What is the probability that Gryffindor scores two or more goals in the first hour? Evaluate this answer numerically.
Let G be the number of Gryffindor goals. Here 
, so 
c) Using the normal approximation, estimate the probability that 100 or more goals (total) are scored in the entire match.
G+S is Poisson with 
, hence roughly normal with 
and 
. 
. But 99.5 is (99.5-88)/9.38 = 1.23 standard deviations above average,
so this probability is 
, or a little under 11%.
Extra Credit) What is the probability that Gryffindor scores more goals than Slytherin? Again, please give a numerical answer.
Since G is roughly normal with mean 48 and standard deviation 
, and S is roughly normal with mean 40 and standard deviation 
. G-S should be roughly normal with mean 8 and standard deviation 
. 
.
Problem 6. Change for a dollar
When I go grocery shopping, I pay a whole number of dollars, and get
back some coins in change. Suppose that the value of these coins is uniformly
distributed between 0 and 1 (dollars). [In reality, the change is a discrete
random variable, with possible values of 0, 0.01, 0.02, up to 0.99. However,
we'll approximate it by a continuous variable that ranges from 0 to 1.]
I go shopping many times, and the change I get on the different days is
denoted 
, 
, etc. You may assume that these variables are independent.
a) Let 
. Find the pdf 
for all values of y.
This is identical to an old homework problem.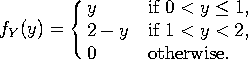 
b) Let 
. Find the expectation and variance of S.
Since
has expectation 1/2 and variance 1/12, S has expectation 24 and
variance 48/12 = 4. Note that the standard deviation of S is 
.
c) Estimate the probability that S > 25.
S needs to be 1/2 standard deviation above average, so this probability
is 
. Note that the continuity correction does NOT apply here, since S is already
continuous.
Problem 7. Parking
A typical Austin parking garage charges $1 for each hour you park, or portion thereof. That is, if you park for less than an hour, you pay $1, if you park for more than an hour but less than two hours you pay $2, and so on.
Let X be the number of hours that a randomly chosen car is in
the garage. The distribution of X is exponential (that is, f(x)
is of the form 
for x>0) with a mean of 3 hours.
a) What is the probability that 
?
Since 
, 
b) What is the probability that a random car's driver will be charged $2?
This is the same as asking the probability that 
, which by a calculation almost identical to that above is 
.
c) Let Y be the cost of parking a car. Is this a continuous or
discrete random variable? What are the possible values of Y? Find
the pdf
.
Y is a discrete random variable that takes on the values 1, 2,
3, etc. 
. This can also be written as 
, where 
, 
.