PROBLEMS:
1. Means and Variances
Let X be a continuous random variable with pdf
(and zero if x is negative). For this problem, you might find
the identity 
useful.
a) Find E(X).
b) Find the variance of X.
c) Find the probability that X < 1.
2. Joint continuous random variable Let X be a uniform
random variable on the interval [0,1], and let Y be a uniform random
variable on the interval [0,2]. (In other words, 
for 0 <x <1, and 
for 0 <y < 2.) Suppose that
X and Y are independent
random variables.
a) Write down the joint pdf 
.
b) Let Z=X+Y. Find the pdf 
. Simplify as much as possible.
c) Find the expectation E(X) and variance Var(X). Repeat for Y.
d) Compute the expectation E(Z) and the variance Var(Z).
3. A silly game. In the (fictional) game of ``dice-flip", each player flips a coin and rolls one die. If the coin comes up tails, his score is the number of dots showing on the die. If the coin comes up heads, his score is twice the number of dots on the die. (E.g., (tails,4) is worth 4 points, while (heads,3) is worth 6 points.) Let X be the first player's score.
a) Compute the pdf 
for all numbers x.
b) Compute the cdf 
for all numbers x.
c) Find the probability that X < 4. Is this the same as 
?
4. Calendar follies. A month of the year is chosen at random (each with probability 1/12). Let X be the number of letters in the month's name, and let Y be the number of days in the month (ignoring leap year). [For the record, January has 31 days, February has 28, March has 31, April has 30, May has 31, June has 30, July has 31, August has 31, September has 30, October has 31, November has 30 and December has 31.]
a) Write down the joint pdf of X and Y. From this, compute the pdf of X and the pdf of Y. (You may want to compile a single table with all this information).
b) Find E(Y).
c) Are the events `` 
" and ``Y=30" independent?
d) Are X and Y independent random variables?
-------------------------------------------
SOLUTIONS
1. Means and Variances
a,b) By the substitution t=2x (don't forget that dx=dt/2), we have
Similarly,
so 
c) Since X is continuous, the probability that X < 1
is the same as the probability that 
, namely
(If you prefer, you can convert the integral back to x and then plug in x=1 and x=0. The answer is of course the same.)
2. Joint continuous random variable
a) The joint pdf is
b) We must integrate 
over the region where it is nonzero. For z <1 this is the region
where x<z, for 1<z<2 it is from x=z-1
to x=z, for 2<z<3 it is from z-1 to 2,
and for z>3 or z<0 it is empty. The result is:
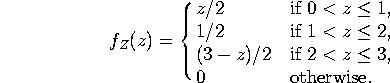
c) We compute: 
, 
, 
. For Y, we either do similar integrals, or just note that Y
has the same distribution as 2X, so E(Y) = 2 E(X)
= 1, Var(Y) = 4 Var(X)=4/12 = 1/3.
d) E(Z)=E(X) + E(Y) = 1/2 + 1 = 3/2. Since X and Y are independent, Var(Z)= Var(X) + Var(Y) = 5/12. You could compute E(Z) and Var(Z) from the density computed in part (b), but that would involve considerable unnecessary work.
3. A silly game.
a) The events (H,1), (H,2), (H,3), (H,4), (H,5), (H,6), (T,1), (T,2), (T,3), (T,4), (T,5), (T,6) each have probability 1/12. The scores 1, 3, 5, 8, 10, and 12 can each be gotten in one and only one way, while 2, 4 and 6 can be gotten in two ways, so
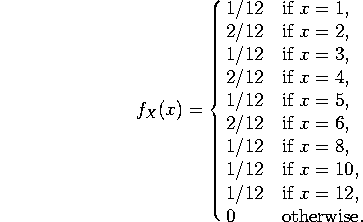
b) Since 
, we have
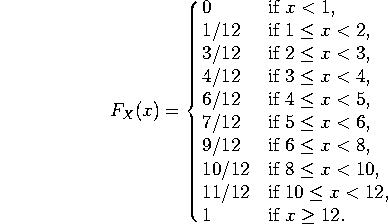
c) 
. Alternatively, 
. This is not the same as
, which is the probability that 
. (The difference between them is the probability that X is EQUAL
to 4.)
4. Calendar follies.
a) The following table sums it up.
is the bottom row, while 
is the last column:
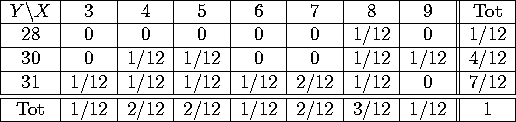
b) Since a year is 365 days, the average month has 365/12 days. More
pedantically, 
.
c) 
, P(Y=30)= 4/12 = 1/3, while 
and Y=30) = 2/12. Since the probability of the intersection equals
the product of the probabilities, the two events ARE independent.
d) No. For the variables X and Y to be independent, EVERY
event involving X has to be independent of EVERY event involving
Y.
It's not hard to see that the events X=5 and Y=28 are not
independent. (Other examples are just as easy to come by.)