M403K Final Exam Solutions
May 10, 2002

Problem 1. Graphing

Consider the function tex2html_wrap_inline95 .

a) Find the partition points of f and make a sign chart for f.

tex2html_wrap_inline101 , so the partition points are 0, tex2html_wrap_inline105 and tex2html_wrap_inline107 . The function is positive for tex2html_wrap_inline109 and for tex2html_wrap_inline111 . It is negative for
tex2html_wrap_inline113 and for tex2html_wrap_inline115 .

b) Find the critical points of f and make a sign chart for f'.

tex2html_wrap_inline121 , so the critical points are -1, 0 and 1. f' is negative for x<-1, positive for -1 < x < 0, negative for 0<x<1 and positive for x>1.

c) Find the inflection points of f and make a sign chart for f''.

tex2html_wrap_inline137 , so the inflection points are at tex2html_wrap_inline139 . f'' is positive for tex2html_wrap_inline143 and for tex2html_wrap_inline145 , and negative for tex2html_wrap_inline147 .

d) On the back of this page, sketch the curve y=f(x). Mark all important points CLEARLY.

I can't draw this on screen, but the graph looks like a ``Mexican hat''. There are local minima at (-1,-1) and (1,-1), and a local maximum at (0,0). The graph is positive, decreasing and curving up for tex2html_wrap_inline109 , then negative, decreasing and curving up for tex2html_wrap_inline159 , hitting a local minimum at (-1, -1). It is then negative, increasing, and curving up for tex2html_wrap_inline161 , and is negative, increasing, and curving down for tex2html_wrap_inline163 , hitting a local maximum at (0,0). The remainder of the graph is a mirror image of the first half, since f(-x)=f(x).

Problem 2. Max-min

Consider the function tex2html_wrap_inline167 .

a) Find all critical points of this function. For each one, say whether it is a local maximum, a local minimum, or neither.

tex2html_wrap_inline169 . Setting this equal to zero we have

displaymath171

But tex2html_wrap_inline173 , so dividing our equation by tex2html_wrap_inline175 gives

displaymath177

so tex2html_wrap_inline179 , so tex2html_wrap_inline181 . This is the ONLY critical point. Now tex2html_wrap_inline183 , and tex2html_wrap_inline185 , so tex2html_wrap_inline187 . Now tex2html_wrap_inline189 , so tex2html_wrap_inline191 , so tex2html_wrap_inline193 is a local minimum.

b) Find the global maximum and minimum of f(x) in the interval [-5,5].

The candidates are the critical points and the endpoints. tex2html_wrap_inline199 is a huge positive number, and tex2html_wrap_inline201 is a tiny negative number, so the maximum is at x=5 and the minimum is at tex2html_wrap_inline205 .

Problem 3. Marginal analysis

The demand x for widgets is related to the price p by the demand equation x = 3000 - 100 p. The cost function is tex2html_wrap_inline213 .

a) Find the marginal cost, the marginal revenue, and the marginal profit at a production level of x=1200.

Solving for price in terms of demand gives p=30 - x/100, so tex2html_wrap_inline219 . Since tex2html_wrap_inline213 , we have a profit tex2html_wrap_inline223 . Taking derivatives we get our marginal quantities:

R'(x) = 30 - x/50, C'(x) = 2-=x/100, P'(x) = 10-x/100.

Finally, plugging in x=1200 gives R'(1200)=6, C'(1200)=8 and P'(1200)=-2. In other words, each additional widget costs us $ 8, and only brings us $ 6 in additional revenue, and so decreases our profit by $ 2.

b) What is the production level that maximizes revenue? What production level maximizes profit?

To maximize revenue, set R'=0. This gives x=1500.

To maximize profit, set P'=0. This gives x=1000.

Problem 4. Exponential growth

An investor invests $1000 at 7% interest, compounded continuously.

a) How much money will he have in 20 years? Express your answer as an exact expression (e.g. something like $ tex2html_wrap_inline247 - no, that's not the right answer), and then approximate it numerically (e.g., $16,000).

tex2html_wrap_inline249 . Now tex2html_wrap_inline251 (the Law of 70, remember?), so tex2html_wrap_inline253 and tex2html_wrap_inline255 . Thus tex2html_wrap_inline257 .

b) When will there be $10,000 in his account? Express your answer as an exact expression. You do NOT need to approximate it numerically.

tex2html_wrap_inline259 , so tex2html_wrap_inline261 , so tex2html_wrap_inline263 , so tex2html_wrap_inline265 . (This is a little under 33 years).

Problem 5. Rates of change

A quantity y is changing at a rate

displaymath269

When x=0, y=5. What does y equal when x=2?

displaymath279

Plugging in y(0)=5 we have tex2html_wrap_inline283 , so C=3. Thus:

displaymath287

Problem 6. Volume

A silo-shaped region is obtained by taking the region between the curve tex2html_wrap_inline289 and the x-axis and rotating it about the y-axis. [See figure]. We compute the volume of this region by slicing it into a stack of disks.

Note: This is a straightforward application of the ``slice and dice principle'', but doesn't directly correspond to any formulas in the book. I'm quite disappointed that only 4 or 5 people in the entire class attempted this problem.

a) Find the (approximate) radius and (approximate) volume of a disk at height y and thickness tex2html_wrap_inline297 .

The radius of the disk is just the value of x on the curve. Since tex2html_wrap_inline289 , we have tex2html_wrap_inline303 , so our radius is tex2html_wrap_inline305 . The area is tex2html_wrap_inline307 , and the volume is (area tex2html_wrap_inline309 thickness) = tex2html_wrap_inline311 .

b) By summing the answer to (a) and taking a limit, express the volume of the silo as a definite integral.

The sum of volumes is of the form tex2html_wrap_inline313 , where tex2html_wrap_inline315 , and y ranges from 0 to 4. Taking the limit as the number of slices goes to infinity gives the definite integral tex2html_wrap_inline319 .

c) Evaluate this integral to get the total volume.

The integral evaluates to tex2html_wrap_inline321 .

Part II:

Evaluate the following. The limits and integrals should be simplified as much as possible, but you don't have to simplify the derivatives:

a) 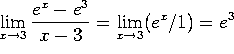tex2html_wrap_inline323

b) 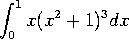tex2html_wrap_inline325 . Set tex2html_wrap_inline327 .

displaymath329

c) tex2html_wrap_inline331

tex2html_wrap_inline333 .

d) tex2html_wrap_inline335 .

e) f'(x), where tex2html_wrap_inline339 . Apply the chain rule twice to get tex2html_wrap_inline341

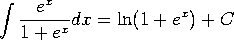f) tex2html_wrap_inline343 . This comes from the substitution tex2html_wrap_inline345 .

g) dy/dx, where 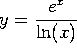tex2html_wrap_inline349 is tex2html_wrap_inline351

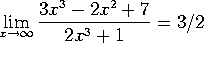h) tex2html_wrap_inline353 . (Either apply L'Hopital 3 times, or divide top and bottom by tex2html_wrap_inline355 and take a limit).

i) 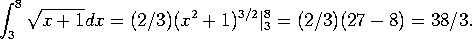tex2html_wrap_inline357 Note that tex2html_wrap_inline359 and that tex2html_wrap_inline361 .

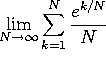j) tex2html_wrap_inline363 . This sum is of the form tex2html_wrap_inline365 , where tex2html_wrap_inline367 and tex2html_wrap_inline369 . Taking the limit gives tex2html_wrap_inline371 , which works out to tex2html_wrap_inline373 .