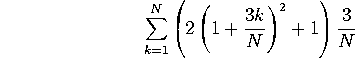, 
.
1. Related rates.
Consider the curve
,
.
a) Find the slope of the line that is tangent to the curve at the point (2,3).
Take the derivative of the equation with respect to x: 
, so 
.
b) A particle is moving along the curve. Its x-coordinate is increasing at a rate of 10 units/second. How fast is y changing when (x,y)=(2,3)?
There are two reasonably easy solutions. One is to use the result from (a): dy/dt = (dy/dx)(dx/dt) = 2(10) = 20 units/second.
The other method is to start from scratch, and take the derivative of the equation with respect to t:
Plugging in values of x, y and dx/dt gives 6 (dy/dt)=120, so dy/dt = 20, as before.
Problem 2. L'Hopital's Rule Evaluate the following limits:
a)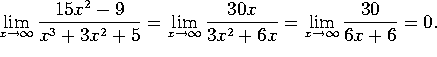 
b)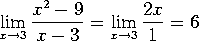 
.
c)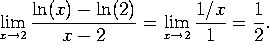 
d)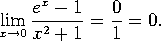 
L'Hopital's rule does not apply here.
Problem 3. Elasticity of Demand
The demand x for a new toy depends on its price p via the demand equation
a) Compute the elasticity of demand E(p) as a function of p.
b) For what values of p is the demand elastic? For what values of p is the demand inelastic?
When p>1, E<-1 and the system is elastic. [Under these circumstances we should lower the price to increase revenue.]
When p<1, E>-1 and the system is inelastic. [To raise revenue, raise the price].
c) What value of p will maximize revenue?
p=1.
Problem 4. Horse sense
For the first two years of life, a pony's height H(t) grows at a rate
(where height is measured in inches and time in years). At age 1, the pony is 45 inches tall.
a) How tall was the pony at birth?
. To evaluate the constant, use the fact that H(1)=45, so 45 = 15
- 1 +
C, so C=31. Now plug back in to get
So when t was zero, H was 31.
b) How tall will the pony be at age 2?
inches.
Problem 5. Indefinite integrals.
Evaluate the following integrals:
a) 
b)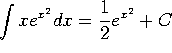 
. (Integrate by substitution with 
.)
c)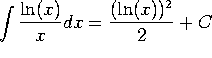 
. (Integrate by substitution with 
.)
d)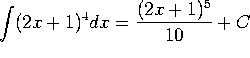 
. (Integrate by substitution with u=2x+1.)
Problem 6. Area under a curve.
We are interested (OK, OK, your instructor is interested) in finding
the area under the curve 
between x=1 and x=4.
a) Estimate this area using 3 rectangles. Your final answer should be an explicit number, like 13 or 152.
Each rectangle has width (4-1)/3 = 1. The three rectangles have height f(2), f(3) and f(4), so the estimated total area is f(2)+f(3)+f(4) = 9+19+33 = 61. [If you used the function values at 1, 2 and 3 instead of 2, 3, and 4, I gave full credit. The answer then would be 31]
b) Estimate the area using N rectangles. You can leave your answer
as a sum, like 
(no, that's not the right answer). Everything in the sum needs to be clearly
defined, but YOU DO NOT NEED TO SIMPLIFY OR EVALUATE THE SUM.
and a=1, so 
. Thus 
, and our estimated area, 
, works out to
