, 
.
1. Related rates.
Consider the curve
,
.
a) Find the slope of the line that is tangent to the curve at the point (2,3).
b) A particle is moving along the curve. Its x-coordinate is increasing at a rate of 10 units/second. How fast is y changing when (x,y)=(2,3)?
Problem 2. L'Hopital's Rule Evaluate the following limits:
a)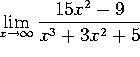 
b)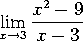 
c)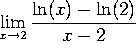 
d)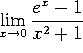 
Problem 3. Elasticity of Demand
The demand x for a new toy depends on its price p via the demand equation
a) Compute the elasticity of demand E(p) as a function of p.
b) For what values of p is the demand elastic? For what values of p is the demand inelastic?
c) What value of p will maximize revenue?
Problem 4. Horse sense
For the first two years of life, a pony's height H(t) grows at a rate
(where height is measured in inches and time in years). At age 1, the pony is 45 inches tall.
a) How tall was the pony at birth?
b) How tall will the pony be at age 2?
Problem 5. Indefinite integrals.
Evaluate the following integrals:
a) 
b) 
c)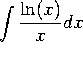 
d) 
.
Problem 6. Area under a curve.
We are interested (OK, OK, your instructor is interested) in finding
the area under the curve 
between x=1 and x=4.
a) Estimate this area using 3 rectangles. Your final answer should be an explicit number, like 13 or 152.
b) Estimate the area using N rectangles. You can leave your answer
as a sum, like 
(no, that's not the right answer). Everything in the sum needs to be clearly
defined, but YOU DO NOT NEED TO SIMPLIFY OR EVALUATE THE SUM.