1. ``Bibonacci'' numbers. The Bibonacci numbers
M328K Final Exam Solutions, May 10, 2003
1. ``Bibonacci'' numbers. The Bibonacci numbers ![]() are defined by
are defined by ![]() ,
, ![]() , and, for n>2,
, and, for n>2, ![]() .
.
a) Prove that, for all positive integers n, ![]() .
.
The proof is by generalized induction. It is true for n=1 and
n=2. Now suppose it is true for all n up to k-1. Then
![]() and
and ![]() , so
, so ![]() .
.
b) Prove that, for all positive integers n, ![]() .
.
The proof is also by generalized induction. It is true for n=1
and n=2. Now suppose it is true for all n up to k-1.
Then ![]() and
and ![]() , so
, so ![]() .
.
Note: The exact formula works out to ![]() , which also can be proven by induction.
, which also can be proven by induction.
2. The following theorem-proof combination is erroneous. Find the errors (there are at least two). Then, rewrite the proof (and, if necessary, the statement of the theorem) so that it really does prove the theorem.
``Theorem'' Every positive integer is divisible by a prime.
``Proof'' Let n be a positive integer. If n is prime, then n is divisible by the prime n, and we are done. If n is composite, then n = ab, where a and b are integers less than n. If a is prime, then a|n, and we are done. If a is composite, write a as a product of two smaller integers, and examine the first of these. Repeat this process, dividing composite factors into products of still smaller factors, and examining the first sub-factor, until you get a factor that cannot be divided further, and is therefore prime.
The first error is that not all positive integers are prime or composite. The integer 1 is neither prime nor composite, and if n is equal to 1, then n isn't divisible by a prime. The second error is that we never show that the process of dividing into factors ever stops. Why can't you keep dividing into smaller factors forever without reaching a prime? The answer requires the Well-Ordering Principle.
Here is a corrected theorem, and two versions of the corrected proof, one using induction and the other using the well-ordering principle directly:
Theorem Every integer greater than 1 is divisible by a prime.
Proof 1 We prove this by induction. It is true for n=2, since 2|2. Now suppose it is true for all n from 2 to k-1. We must show that k is divisible by a prime. If k is prime, then k is divisible by the prime k, and we are done. If k is not prime, it must be composite, since k;SPMgt;1. Thus k=ab, where a and b are integers less than k and greater than 1. By the inductive hypothesis, a is divisible by a prime p, hence k is also divisible by p.
Proof 2 Let n be a positive integer greater than one.
If n is prime, then n is divisible by the prime n,
and we are done. If n is composite, then ![]() , where
, where ![]() and
and ![]() are integers less than n. If
are integers less than n. If ![]() is prime, then
is prime, then ![]() , and we are done. If
, and we are done. If ![]() is composite, write
is composite, write ![]() as a product of two integers, each bigger than 1 and smaller than
as a product of two integers, each bigger than 1 and smaller than ![]() , and examine the first factor
, and examine the first factor ![]() . Repeat this process, dividing composite factors into products of still
smaller factors, and examining the first sub-factor. The set
. Repeat this process, dividing composite factors into products of still
smaller factors, and examining the first sub-factor. The set ![]() is nonempty. By the Well-Ordering Principle, this set has a smallest elements
is nonempty. By the Well-Ordering Principle, this set has a smallest elements
![]() . This implies that
. This implies that ![]() is prime, for if
is prime, for if ![]() were composite,
were composite, ![]() would exist and would be smaller than
would exist and would be smaller than ![]() . Since
. Since ![]() , n is divisible by a prime.
, n is divisible by a prime.
3. Matrix products. It is a known fact that, if A and B
are matrices such that the product AB makes sense, then ![]() . (That is, the transpose of the product is the product of the transposes,
in the opposite order). Taking this fact as given, prove the following statement:
. (That is, the transpose of the product is the product of the transposes,
in the opposite order). Taking this fact as given, prove the following statement:
Claim: Let n;SPMgt;1 and let ![]() be an ordered n-tuple of matrices such that the product
be an ordered n-tuple of matrices such that the product ![]() is defined. Then
is defined. Then ![]() , i.e., the transpose of the product is the product of the transposes with
the order reversed.
, i.e., the transpose of the product is the product of the transposes with
the order reversed.
This is yet another proof by induction on n. (In this case it
is regular induction, not generalized induction). The base case is n=2,
which is given. Now suppose it is true for n=k-1. Then ![]() . Take
. Take ![]() and
and ![]() . Then
. Then ![]() .
.
4. a) Find the greatest common factor of 50 and 76.
b) Write this number as a linear combination of 50 and 76.
Use the Euclidean algorithm:
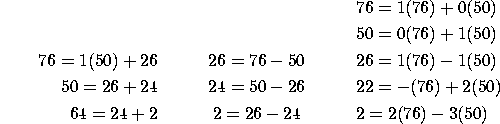
So (50,76)=2=2(76)-3(50)
c) Find all solutions, mod 76, of the equation ![]() .
.
Since (-3)50 = 2 (mod 76), we must have -27 (50) = 18 (mod 76). The solution is only defined mod 76/(76,50) = 38, so the solutions mod 76 are 11 and 49.
5. a) Find all solutions, in the range ![]() , to the following system of congruences.
, to the following system of congruences.
![]()
Use the Euclidean argument to get that 1 = 4(49) - 13(15) = 196 - 195.
A solution is therefore ![]() (mod 735).
(mod 735).
b) Find all solutions, in the range ![]() , to the system of congruences
, to the system of congruences

Use the Euclidean algorithm on the first two equations to get x=33 (mod 35). Combine that with the third equation to get x=68 (mod 385). Combine that with the last equation to get x=838 (mod 5005).
6. a) Compute ![]() (mod 101). (Note that 101 is prime)
(mod 101). (Note that 101 is prime)
Since ![]() , we only care about 883 (mod 100), so we can take the 83rd power instead
of the 883rd. By successive squaring (and reduction mod 101), we have
, we only care about 883 (mod 100), so we can take the 83rd power instead
of the 883rd. By successive squaring (and reduction mod 101), we have ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Then
. Then ![]()
b) You are told that ![]() (mod 101) and that
(mod 101) and that ![]() . Find a positive integer d such that
. Find a positive integer d such that ![]() .
.
We seek an inverse to 83 (mod 100). By the Euclidean algorithm (again!)
we get ![]() (note that
(note that ![]() .) So d=47.
.) So d=47.
c) If y=24, what is x? By successive squaring, we get
![]() . You can check directly, again by successive squaring, that
. You can check directly, again by successive squaring, that ![]() .
.
7. Let n=8999271. a) What is the prime factorization of n? (Hint: n is the product of more than two primes) You may use your calculators, but you may NOT use a ``factor'' key or function, and you MUST show how you did the factorization in order to receive credit.
It's clear that 9|n, so we factor that out to get n=9m,
where m=999919. Using Fermat's method we see that this is ![]() . Both 991 and 1009 are prime, so our factorization is
. Both 991 and 1009 are prime, so our factorization is ![]()
b) Compute ![]() .
.
![]() .
.
c) Somebody suggests coding numbers by ![]() , where x is relatively prime to n. Find a key that decodes
this (i.e., a number k such that
, where x is relatively prime to n. Find a key that decodes
this (i.e., a number k such that ![]() .
.
By the Euclidean argument, ![]() , so
, so ![]() , so our answer is -352207 (mod
, so our answer is -352207 (mod ![]() ). The smallest positive representative is
). The smallest positive representative is ![]() .
.
[In fact, the smaller key k' = 55440 will also work. 17 k'
isn't equal to 1 mod ![]() , but it is equal to 1 mod the least common multiple of 990, 1008 and 6,
so taking things to the 17k' power preserves their residue class
mod 9, mod 991, and mod 1009, and hence mod n.]
, but it is equal to 1 mod the least common multiple of 990, 1008 and 6,
so taking things to the 17k' power preserves their residue class
mod 9, mod 991, and mod 1009, and hence mod n.]