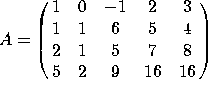 and let
and let 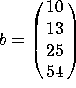 . The augmented matrix [A b] is row-equivalent to
. The augmented matrix [A b] is row-equivalent to 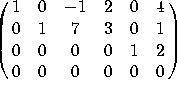 .
.
1. Let 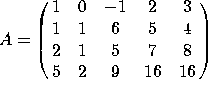 and let
and let 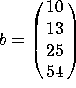 . The augmented matrix [A b] is row-equivalent to
. The augmented matrix [A b] is row-equivalent to 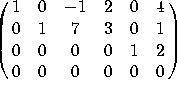 .
.
a) Find all solutions to Ax=b. Express your answers in parametric form.
b) Find a basis for the column space of A.
c) Find a basis for the null space of A.
d) Find a basis for ![]() .
.
2. For each of these matrices, (i) find the determinant, (ii) state whether the matrix is invertible, and (iii) either find the inverse of the matrix (if it is invertible) or find a nonzero solution to Ax=0 (if it isn't).
a) ![]()
b) 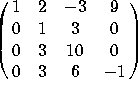 .
.
3. In the space ![]() of quadratic polynomials, let
of quadratic polynomials, let ![]() be the standard basis, and let
be the standard basis, and let ![]() be an alternate basis
be an alternate basis
a) Find the change-of-basis matrix ![]() that converts from coordinates in the B basis to coordinates in
the E basis.
that converts from coordinates in the B basis to coordinates in
the E basis.
b) Find the change-of-basis matrix ![]() that converts from coordinates in the E basis to coordinates in
the B basis.
that converts from coordinates in the E basis to coordinates in
the B basis.
c) Compute the coordinates, in the B basis, of the following four
vectors: ![]()
4. Let ![]() be defined by
be defined by 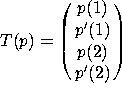 , where p' is the derivative of p with respect to t.
Find the matrix of this linear transformation relative to the standard
basis.
, where p' is the derivative of p with respect to t.
Find the matrix of this linear transformation relative to the standard
basis.
5. a) Find a ![]() matrix A whose eigenvalues are 1, 0 and -1, and whose corresponding
eigenvectors are
matrix A whose eigenvalues are 1, 0 and -1, and whose corresponding
eigenvectors are ![]() ,
, ![]() and
and ![]() .
.
b) Compute ![]() .
.
6. In this problem, we model the spread of an epidemic. Let S(k) be the number of sick people in week k, and let I(k) be the number of people who are infected, but not yet sick. Each week, a sick person will infect 6 others, while an infected person will become sick. (In our model, nobody ever recovers or dies). That is,
![]()
Letting ![]() , this boils down to
, this boils down to ![]() .
.
a) Find the eigenvalues and corresponding eigenvectors of the matrix.
b) In the long run, what will be the ratio of sick to infected (but not yet sick) people?
c) If there are 3 sick people and 1 infected person in week zero, how many sick and infected people will there be in week k?
7. Let 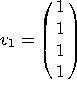 ,
, 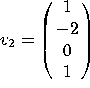 , and
, and 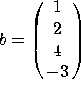 . Let
. Let ![]() .
.
a) Compute ![]() .
.
b) Find the distance from b to the plane V.
c) Find a least-squares solution to 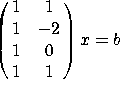 .
.
8. a) Find an orthogonal basis for the column space of 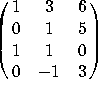 .
.
b) Find the projection of ![]() onto this space.
onto this space.
9. True-False. Indicate whether each of these statements is true or false. If a statement is sometimes true and sometimes false, write ``false''. You do NOT have to justify your answers. There is no penalty for wrong answers, so go ahead and guess if you are unsure of your answer.
a) The equation Ax=b has a solution if, and only if, b is in the span of the columns of A.
b) The equation Ax=b has a solution if, and only if, the augmented matrix [A b] has a pivot position in each row.
c) If the ![]() matrix A has a pivot in each column, then the columns of A
are linearly independent.
matrix A has a pivot in each column, then the columns of A
are linearly independent.
d) If the ![]() matrix A has a pivot in each column, then the columns of A
spen
matrix A has a pivot in each column, then the columns of A
spen ![]() .
.
e) Every linear transformation from ![]() to
to ![]() can be represented by an
can be represented by an ![]() matrix.
matrix.
f) If A, B and C are matrices such that the product
ABC makes sense, then ![]() .
.
g) If the determinant of a square matrix A is zero, then A is invertible.
h) Given vectors ![]() , the set of all linear combinations of these vectors is a subspace of
, the set of all linear combinations of these vectors is a subspace of
![]() .
.
i) If two matrices are row-equivalent, then their column spaces have the same dimension.
j) The row space of a matrix has the same dimension as the column space.
k) ![]() is a subspace of
is a subspace of ![]() .
.
l) The range of T(x) = Ax is the same as the column space of A.
m) If ![]() , then
, then ![]() is a basis for H.
is a basis for H.
n) The dimension of the null space of a matrix is the number of free variables in the equation Ax=0.
o) If A is a ![]() matrix, then the null space of A is at least 2-dimensional.
matrix, then the null space of A is at least 2-dimensional.
p) A number c is an eigenvalue of A if and only if det(A-cI)=0.
q) If the characteristic polynomial of a ![]() matrix A is
matrix A is ![]() , then A is diagonalizable.
, then A is diagonalizable.
r) Every ![]() matrix has at least one eigenvalue, but it may be complex.
matrix has at least one eigenvalue, but it may be complex.
s) If ![]() , with D diagonal, then each column of P is an eigenvector
of A.
, with D diagonal, then each column of P is an eigenvector
of A.
t) If Ax=0, then x is in ![]() .
.
u) If two nonzero vectors are orthogonal, they are linearly independent.
v) If two nonzero vectors are linearly independent, they are orthogonal.
w) If ![]() , where
, where ![]() and
and ![]() , then
, then ![]() .
.
x) The equation Ax=b always has a least-squares solution, no matter what A and b are.
y) If ![]() , then Ax=b has a unique least-squares solution.
, then Ax=b has a unique least-squares solution.