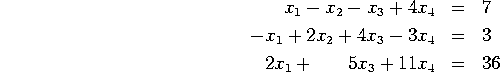
1. Find all solutions to the system of equations:
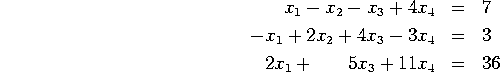
Is the set of solutions empty, a point, a line, a plane, or some other geometric shape? If it is a line or a plane, express this set in parametric form.
The augmented matrix reduces to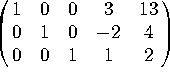 
. There is one free variable, so the solutions form a line, which can
be parametrized as
.
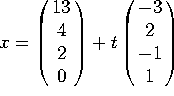2. Consider the matrix and vector
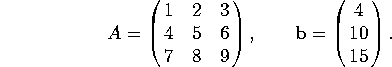
a) Is 
in the span of the columns of A? If so, write
explicitly as a linear combinations of the columns.
The augmented matrix [A | b] reduces to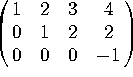 
. Thus there are no solutions to 
, so
is NOT a linear combination of the columns of A.
b) Are the columns of A linearly independent? If not, write the zero vector as a nontrivial linear combination of the columns of A.
A by itself row-reduces to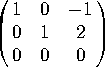 
, so Ax=0 boils down to 
, 
, 
free. Setting 
gives the solution 
. That is, 
.
3. Consider the linear transformation 
given by
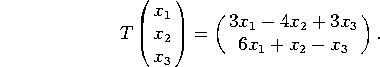
a) Find the matrix of T.
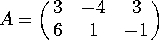
b) Is T one-to-one? Why or why not?
Row reducing A gives two pivots. Since there are 3 columns, there is a free variable, so T is NOT one-to-one.
c) Is T onto? Why or why not?
There is a pivot in each row, so T is onto.
4. Indicate whether each of these matrices is invertible. If it is, find the inverse. If it isn't invertible, explain why.
a)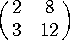 
The determinant is 
, so the matrix is NOT invertible.
b)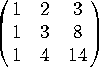 
By row-reducing 
you get 
, where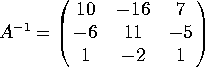 
5. Indicate whether each of these statements is true or false. If a statement is sometimes true and sometimes false, write ``false''. You do NOT have to justify your answers. There is no penalty for wrong answers, so go ahead and guess if you are unsure of your answer.
a) The columns of a 
matrix must be linearly dependent.
True. There are at most 4 pivots, which cannot fill out 5 columns
b) The columns of a
matrix must span 
.
False. There may be fewer than 4 pivots.
c) If two matrices A and B have different sizes, then the sum A + B is not defined.
True.
d) If two matrices A and B have different sizes, then the product AB is not defined.
False. A and B don't have to be the same size. Rather, the WIDTH of A must match the HEIGHT of B.
e) If A and B are inverses, then AB=BA.
True. AB=BA=I
f) If a set 
of 2 or more vectors is linearly dependent, then one of the vectors is
a linear combination of the others.
True. We proved this in class.
g) If the columns of a 
matrix are linearly independent, then they span
.
True. If the columns are linearly independent, then there are 4 pivots,
so there is a pivot in each row, so the columns span
.
h) If the columns of an 
matrix are linearly independent, then they span 
.
False. If 
, then having pivots in each column does NOT equate to having pivots in
each row.
i) If a 
matrix A has exactly 3 pivots, then the linear transformation 
is one-to-one.
True. There are pivots in each column, hence there are no free variables.
j) If a
matrix A has exactly 3 pivots, then the linear transformation
is onto.
False. One row doesn't have a pivot.