matrices are row-equivalent:
1. The following two
matrices are row-equivalent:
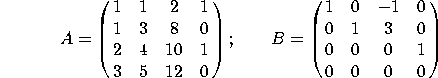
a) What is the rank of A?
There are 3 pivots, so the rank is 3.
b) Find a basis for the column space of A.
The pivots are in the 1st, 2nd and 4th columns, so a basis is
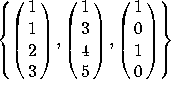. Note that the 1st, 2nd and 4th columns of B are NOT a basis for
Col(A). They are a basis for Col(B).
c) Find a basis for the null space of A.
After row-reduction our equations become: 
, 
, 
, and 
, so all solutions are multiples of the single basis vector 
.
d) Find a basis for the row space of A.
Since Row(A)=Row(B), our basis is 
. Note that the first three rows of A are NOT a basis, as the third
is the sum of the first two.
2. Let V=Span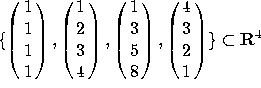 
.
a) What is the dimension of V?
V is the column space of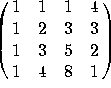 
, which row-reduces to 
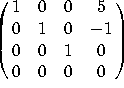. There are 3 pivots, so the dimension is 3.
b) Find a basis for V.
The pivots are in the first 3 columns, so the first three vectors will
do, namely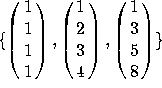 
c) Let W be the subspace of 
spanned by the polynomials 
, 
, 
and 
. What is the dimension of W? Find a basis for W.
Once you write down the coordinates, this is the EXACT SAME PROBLEM.
The dimension is 3, and the basis is the set of vectors whose coordinates
are the answer to part (b), namely 
.
3. Consider the following basis for 
:
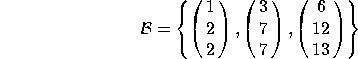
a) Find the change-of-basis matrix 
that converts from coordinates in the B basis to coordinates in
the standard (E) basis.
The columns of
are just the vectors themselves:
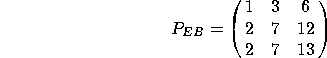
b) Find the change-of-basis matrix 
that converts from coordinates in the standard basis to coordinates in
the B basis.
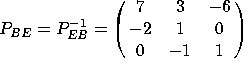, as computed by row-reducing 
.
c) Let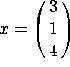 
. Compute 
.
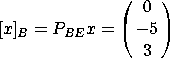. You can check that x is indeed equal to 
.
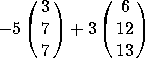d) Consider the basis 
, 
, 
for the vector space 
. Find the coordinates of the polynomial 
in this basis.
Once you write this in coordinates (with respect to the standard basis),
this is the same problem as (c), and has the same answer: 
4. a) Are the polynomials 
, 
and 
linearly independent?
Use coordinates to convert this into a problem in
. Row-reducing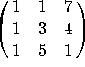 
gives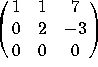 
, which only has 2 pivots. Since there is not a pivot in the last column,
the three vectors are NOT linearly independent.
b) Do the polynomials 
, 
and 
span
?
Likewise, use coordinates. The matrix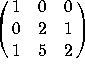 
DOES row-reduce to something with a pivot in each row, so the vectors
DO span the space. (Instead of row-reducing, you could also compute the determinant).
5. Indicate whether each of these statements is true or false. If a statement is sometimes true and sometimes false, write ``false''. You do NOT have to justify your answers. There is no penalty for wrong answers, so go ahead and guess if you are unsure of your answer.
a) The rank of a matrix is the dimension of its row space.
TRUE. It's also the dimension of the column space.
b) Let 
be vectors in a vector space V. For Span 
to be a subspace of V, the vectors must be linearly independent.
FALSE. If the vectors are linearly dependent, then the dimension of
Span
will be less than 3, but it will still be a subspace.
c) If A and B are row-equivalent matrices, then Col(A)=Col(B).
FALSE. See Problem 1 for a counterexample.
d) If A and B are row-equivalent matrices, then Null(A)=Null(B).
TRUE. The equations Ax=0 and Bx=0 are equivalent.
e) If A and B are row-equivalent matrices, then Row(A)=Row(B).
TRUE. The rows of each can be obtained from the rows of the other.
f) Let 
be a collection of four vectors in 
. One of the 
's can be written as a linear combination of the others.
TRUE.
has dimension 3, so any collection of 4 or more vectors is linearly dependent,
so one of the vectors is a linear combination of the others.
g) If a collection of five polynomials spans 
, then it forms a basis for
.
FALSE.
is only 4-dimensional, so any collection of 5 vectors will fail to be
linearly independent.
h) Every change-of-basis matrix is invertible.
TRUE. The inverse of P_{BC} is P_{CB}.
i) If a linearly dependent set of vectors spans
, then there must be at least 4 vectors in the set.
TRUE. A linearly dependent set of 3 (or fewer) vectors can't span
.
j) If 
is a linearly independent set of vectors in V, and 
is a spanning set for V, then n>k.
FALSE. All you can say is that 
.