matrix
1. Consider the
matrix
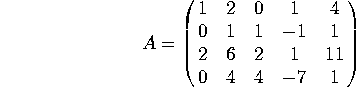
a) What is the rank of A? [Note: the row reduction of A can be done using integers only. If you start getting fractions, you probably made a mistake]
b) Find a basis for the column space of A.
c) Find a basis for the null space of A.
2. Consider the linear transformation 
defined by
.
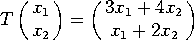a) Find the matrix of this linear transformation.
b) Is T one-to-one? Is T onto?
c) Let S be a rectangle whose area is 2. What is the area of T(S)?
3. Compute the following determinants:
a)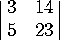 
b)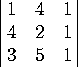 
c)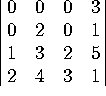 
4. Consider the matrix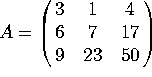 
, that factorizes as A = LU, where 
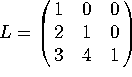and 
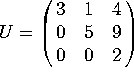. Let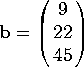 
. Solve the problem 
in two steps (Note: you do NOT get any credit for solving the full equations
directly):
a) Solve 
for 
, and then
b) Solve 
for 
. Does this solution also satisfy
?
5. Indicate whether each of these statements is true or false. If a statement is sometimes true and sometimes false, write ``false''. You do NOT have to justify your answers. There is no penalty for wrong answers, so go ahead and guess if you are unsure of your answer.
a) The rank of a matrix is the dimension of its null space.
b) Swapping two rows of a matrix does not change the determinant of that matrix.
c) If A and B are square matrices of the same size, then
.
d) If an 
matrix has an inverse, then the columns of that matrix span 
.
e) If the determinant of a (square) matrix is zero, then its columns are linearly dependent.
f) The span of 3 vectors in
is a 3-dimensional subspace of
.
g) Let A be an 
matrix. The dimension of Col(A) plus the dimension of Null(A)
equals 5.
h) If two vectors 
and 
lie in a subspace H of
, then every linear combination of
and
also lies in H.
i) If a 
matrix has rank 3, then its null space is 1-dimensional.
j) A basis for a subspace H is a linearly independent set of vectors whose span is H