matrices are row-equivalent:
1. The following two
matrices are row-equivalent:
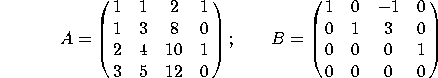
a) What is the rank of A?
b) Find a basis for the column space of A.
c) Find a basis for the null space of A.
d) Find a basis for the row space of A.
2. Let V=Span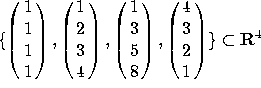 
.
a) What is the dimension of V?
b) Find a basis for V.
c) Let W be the subspace of 
spanned by the polynomials 
, 
, 
and 
. What is the dimension of W? Find a basis for W.
3. Consider the following basis for 
:
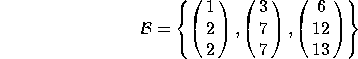
a) Find the change-of-basis matrix 
that converts from coordinates in the B basis to coordinates in
the standard (E) basis.
b) Fina the change-of-basis matrix 
that converts from coordinates in the standard basis to coordinates in
the B basis.
c) Let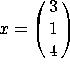 
. Compute 
.
d) Consider the basis 
, 
, 
for the vector space 
. Find the coordinates of the polynomial 
in this basis.
4. a) Are the polynomials 
, 
and 
linearly independent?
b) Do the polynomials 
, 
and 
span
?
5. Indicate whether each of these statements is true or false. If a statement is sometimes true and sometimes false, write ``false''. You do NOT have to justify your answers. There is no penalty for wrong answers, so go ahead and guess if you are unsure of your answer.
a) The rank of a matrix is the dimension of its row space.
b) Let 
be vectors in a vector space V. For Span 
to be a subspace of V, the vectors must be linearly independent.
c) If A and B are row-equivalent matrices, then Col(A)=Col(B).
d) If A and B are row-equivalent matrices, then Null(A)=Null(B).
e) If A and B are row-equivalent matrices, then Row(A)=Row(B).
f) Let 
be a collection of four vectors in 
. One of the 
's can be written as a linear combination of the others.
g) If a collection of five polynomials spans 
, then it forms a basis for
.
h) Every change-of-basis matrix is invertible.
i) If a linearly dependent set of vectors spans
, then there must be at least 4 vectors in the set.
j) If 
is a linearly independent set of vectors in V, and 
is a spanning set for V, then n>k.