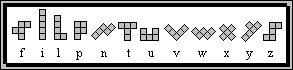
Pentominoes are shapes that use five square blocks joined edge to edge to form various combinations. There are twelve possible shapes in a set of unique pentominoes, named T, U, V, W, X, Y, Z, F, I, L, P, and N. An easy way to remember all the letters in a pentominoes set is to look at the word, FILiPiNo, and remember the end of the alphabet, TUVWXYZ. Pentominoes are said to have been "invented" by Solomon W. Golomb in 1953 at a talk he gave to the Harvard Mathematics Club. Although he came up with the name, pentominoes have been around since a much earlier time. The first pentomino problem, written by the great English inventor of puzzles, Henry Ernest Dudeny, was published in 1907 in the Canterbury Puzzles.
The twelve pentominoes are often referred to by the letters they resemble.

There are about as many puzzles and games using pentominoes as there are people who play with them. Here are a few examples. There are many more puzzles and solutions all over the internet and in the book Polyominoes by Solomon Golomb.
Each of the twelve pentominoes can be modeled two-dimensionally with nine of the remaining pentominoes. To do this, first pick up a piece to model and put it aside as this piece will not be necessary for the scaled model. Second, try to construct a duplicate on a 3/1 scale. The new model will only need nine pieces.
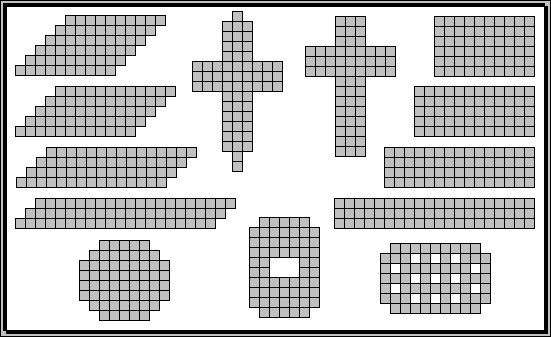
Try to fit your pentominoes together to make one of the following shapes. Notice that your set of pentominoes has 60 squares in all, so we can try to tile rectangles of dimensions 1x60, 2x30, 3x20, 4x15, 5x12 and 6x10. Of these, the formats 1x60 and 2x30 can not be covered with the 12 pentominoes, for obvious reasons (consider the 'X, piece, for example, which is 3 units wide in every direction). The number of solutions for each of the rectangles is:
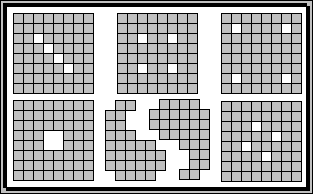
Besides its intrigue as a puzzle, the placement of pentominoes on a checkerboard also makes it an exiting competitive game of skill. Played by two or three players, the object of the game is to be the last player to place a pentomino piece on the checkerboard. Players take turns choosing a piece and placing it on the board. The pieces must not overlap or extend beyond the boundary of the board, but they do not have to be adjacent. The game will last at least five, and at the most twelve moves and it has more opening moves than chess. Can you demonstrate a game that only lasts five moves? (assuming both players are doing their best of course.)
The figures shown are known as pentomino checkerboards and are constructed two dimensionally (lying the pieces flat). Note that one of them forms a Yin Yang symbol when you put the two equal halves together. Here, you can make your own puzzle by selecting any four squares on the checkerboard to leave blank.
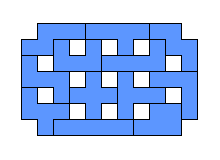
|
The following is different from the previous tiling problem. We try to form a fence with the 12 pentominoes encompassing a empty field. The pentominoes along the fence must be connected along a side. There are four shapes, in each of them we try to maximize the area of the field.
A solution of problem 1 is presented below. It has been proved maximum.
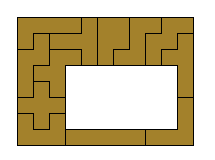
|
By making a set of pentominoes out of cubes instead of squares, you can try to solve many more puzzles. (Wooden cubes are sold at most craft stores, but try to make sure that they are of uniform sizes.) The first puzzle with these solid pentominoes is to be able to put them into a 3x4x5 box. Ten of the twelve pentominoes can be modeled three-dimensionally with all twelve pieces. Construct the pentomino figures on a 2/1 scale, but this time around a new dimension is added -- they must be three stories tall! This technique is fiendishly difficult as the pentominoes can be used any which way that works. Keep in mind that there are two pentominoes that cannot be constructed in this manner -- the W and the X.
