


Next: Sparse Matrix Storage
Up: ITPACK 2C: A FORTRAN
Previous: ITPACK 2C: A FORTRAN
Introduction
For several years, we have been involved with the development and use of
research-oriented programs using iterative algorithms for solving large
sparse linear systems
Au = b
with positive diagonal elements. One solves for the N component
unknown vector u given the
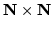 nonsingular
coefficient matrix A and the N component right-hand side vector
b. The current ITPACK software package of subroutines, version 2C,
provides for the use of seven alternative iterative procedures. While
these subroutines are not designed as production software, they should
successfully handle industrial problems of moderate size, that is, ones
that fit in high-speed memory. This package is written in standard
FORTRAN-66 code. It has been tested over a wide variety of computer
systems using various FORTRAN compilers, including one which is
FORTRAN-77 compatible (see Acknowledgements).
The seven iterative solution modules are based on several basic
iterative procedures, such as the Jacobi method, the Successive
Overrelaxation (SOR) method, the Symmetric SOR (SSOR) method, and the RS
method for the reduced system. With the exception of SOR, the
convergence of these basic methods are accelerated by Chebyshev
(Semi-Iteration, SI) or Conjugate Gradient (CG) acceleration. All
methods are available with adaptive parameter estimation and automatic
stopping tests. When using the RS method it is required that the linear
system be reordered into a ``red-black"4
system [6,12]. A switch to compute, if possible, the red-black
indexing, permute the linear system, and permute associated vectors is
provided.
The successful convergence of iterative methods may be dependent on
conditions that are difficult to determine in advance. For example,
determining whether the coefficient matrix is positive definite can be
as costly to check as solving the system. On the other hand, some
conditions affecting convergence, such as positive diagonal elements,
diagonal dominance, and symmetry are relatively easy to verify. For
some applications, the theory may not exist to guarantee the convergence
of an iterative method. The algorithms in ITPACK have been tested most
extensively for linear systems arising from elliptic partial
differential equations. The routines can be applied, formally, to any
linear system which fits in high-speed memory. However, rapid
convergence, and indeed convergence itself cannot be guaranteed unless
the matrix of the system is symmetric and positive definite. Success
can be expected, though not guaranteed, for mildly nonsymmetric systems.
In other words, iterative methods may not converge when applied to
systems with coefficient matrices which are completely general with no
special properties.
This article discusses the usage of ITPACK and gives a few test
results. The description of the iterative methods is given in [4].
The underlying theory on which the iterative algorithms are based is
described in [6]. A survey of the iterative methods in ITPACK
is presented in [11].
Throughout this paper, we adopt notation such as SOR() when
referring to a subroutine and A(*) for a single-dimensioned array.
The residual vector is
b-Au(n) for the linear system Au=b and the
pseudo-residual vector is
Gu(n)+k-u(n) for a basic iterative
method of the form
u(n+1)=Gu(n)+k. The smallest and
largest eigenvalues of the iteration matrix G are denoted m(G) and
M(G), respectively.
nonsingular
coefficient matrix A and the N component right-hand side vector
b. The current ITPACK software package of subroutines, version 2C,
provides for the use of seven alternative iterative procedures. While
these subroutines are not designed as production software, they should
successfully handle industrial problems of moderate size, that is, ones
that fit in high-speed memory. This package is written in standard
FORTRAN-66 code. It has been tested over a wide variety of computer
systems using various FORTRAN compilers, including one which is
FORTRAN-77 compatible (see Acknowledgements).
The seven iterative solution modules are based on several basic
iterative procedures, such as the Jacobi method, the Successive
Overrelaxation (SOR) method, the Symmetric SOR (SSOR) method, and the RS
method for the reduced system. With the exception of SOR, the
convergence of these basic methods are accelerated by Chebyshev
(Semi-Iteration, SI) or Conjugate Gradient (CG) acceleration. All
methods are available with adaptive parameter estimation and automatic
stopping tests. When using the RS method it is required that the linear
system be reordered into a ``red-black"4
system [6,12]. A switch to compute, if possible, the red-black
indexing, permute the linear system, and permute associated vectors is
provided.
The successful convergence of iterative methods may be dependent on
conditions that are difficult to determine in advance. For example,
determining whether the coefficient matrix is positive definite can be
as costly to check as solving the system. On the other hand, some
conditions affecting convergence, such as positive diagonal elements,
diagonal dominance, and symmetry are relatively easy to verify. For
some applications, the theory may not exist to guarantee the convergence
of an iterative method. The algorithms in ITPACK have been tested most
extensively for linear systems arising from elliptic partial
differential equations. The routines can be applied, formally, to any
linear system which fits in high-speed memory. However, rapid
convergence, and indeed convergence itself cannot be guaranteed unless
the matrix of the system is symmetric and positive definite. Success
can be expected, though not guaranteed, for mildly nonsymmetric systems.
In other words, iterative methods may not converge when applied to
systems with coefficient matrices which are completely general with no
special properties.
This article discusses the usage of ITPACK and gives a few test
results. The description of the iterative methods is given in [4].
The underlying theory on which the iterative algorithms are based is
described in [6]. A survey of the iterative methods in ITPACK
is presented in [11].
Throughout this paper, we adopt notation such as SOR() when
referring to a subroutine and A(*) for a single-dimensioned array.
The residual vector is
b-Au(n) for the linear system Au=b and the
pseudo-residual vector is
Gu(n)+k-u(n) for a basic iterative
method of the form
u(n+1)=Gu(n)+k. The smallest and
largest eigenvalues of the iteration matrix G are denoted m(G) and
M(G), respectively.



Next: Sparse Matrix Storage
Up: ITPACK 2C: A FORTRAN
Previous: ITPACK 2C: A FORTRAN