


Next: Notes on Use
Up: ITPACK 2C: A FORTRAN
Previous: Examples
Numerical Results
The iterative algorithms in ITPACK have been tested over a wide class
of matrix problems arising from elliptic partial differential equations
with Dirichlet, Neumann, and mixed boundary conditions on arbitrary
two-dimensional regions (including cracks and holes) and on rectangular
three-dimensional regions [1]. Both finite-difference and
finite-element procedures have been employed to obtain the linear systems.
The two sample problems presented here, while simple to pose, are
representative of the behavior of the ITPACK routines for more complex
problems. The iterative algorithms make no use of the constant
coefficients in these two problems or of the particular structure of the
resulting linear system. Because the ITPACK code is not tailored to any
particular class of partial differential equations or discretization
procedure, but rather to sparse linear systems, it is felt that the
package can be used to solve a wider class of problems.
We now consider two simple partial differential equations which when
discretized by finite-difference methods give rise to large sparse
linear systems. We obtain the solution of each of these systems by the
seven algorithms in ITPACK 2C. These numerical results should aid the
user of ITPACK in determining the amount of time required when solving
more complicated sparse systems. However, one should not interpret
these execution times as conclusive by themselves. Variances introduced
by different compilers, computer systems, and timing functions can
sometimes be significant. Moreover, the number of iterations required
by an iterative method is dependent on the problem being solved, the
initial estimate for the solution, the parameter estimates used, and the
relative accuracy requested in the stopping criterion RPARM(1).
These tests were run on the CDC Cyber 170/750 at the University of Texas
with the FTN 4.8 compiler (OPT=2).
To obtain representative sparse linear systems, we discretize the
following two self-adjoint elliptic partial differential equations in a
region with prescribed conditions on the boundary. Here uxx,
uyy, uzz are partial derivatives and du/dn is the derivative
in the normal direction.
| uxx + 2uyy = 0, |
|
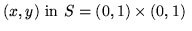 |
(1) |
| u = 1 + xy, |
|
 |
|
Using the standard 5-point symmetric finite-difference operator with
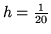 , we obtain a sparse linear system with 1729 nonzero
elements and 361 unknowns.
, we obtain a sparse linear system with 1729 nonzero
elements and 361 unknowns.
| uxx+2uyy+3uzz=0, |
|
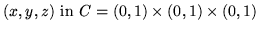 |
|
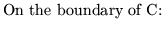 |
|
|
(2) |
| u=1, |
|
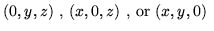 |
|
| du/dn = yz(1 + yz), |
|
(1,y,z) |
|
| du/dn = xz(1 + xz), |
|
(x,1,z) |
|
| du/dn = xy(1 + xy), |
|
(x,y,1) |
|
Using the standard 7-point symmetric finite difference operator with
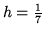 , we obtain a sparse linear system with 1296 nonzero
elements and 216 unknowns.
Tables 1 and 2 display the number of iterations and
execution times (in seconds) for the seven methods in ITPACK 2C for the
linear systems corresponding to problems (1) and (2), respectively, using
symmetric sparse storage. Both the time for the iteration algorithm and
the total time for the subroutine call are given. The stopping criterion
was set to
, we obtain a sparse linear system with 1296 nonzero
elements and 216 unknowns.
Tables 1 and 2 display the number of iterations and
execution times (in seconds) for the seven methods in ITPACK 2C for the
linear systems corresponding to problems (1) and (2), respectively, using
symmetric sparse storage. Both the time for the iteration algorithm and
the total time for the subroutine call are given. The stopping criterion
was set to
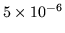 . To illustrate how effective the adaptive
procedures are, we have included in these tables the number of iterations
and the time when the optimum iteration parameters were used with no
adaptive procedures.
. To illustrate how effective the adaptive
procedures are, we have included in these tables the number of iterations
and the time when the optimum iteration parameters were used with no
adaptive procedures.
Table 1:
Number of Iterations and Execution Times for
Problem (1) Using Adaptive and Nonadaptive
Procedures (Nonadaptive Data in Parentheses)
| Routine |
Ordering |
Iterations |
Iteration time |
Total time |
| JCG() |
Natural |
61 (61) |
.250 (.247) |
.281 (.271) |
| |
Red-black |
61 (61) |
.232 (.246) |
.402 (.413) |
| |
|
|
|
|
| JSI() |
Natural |
108 (95) |
.408 (.344) |
.439 (.375) |
| |
Red-black |
108 (95) |
.393 (.332) |
.569 (.498) |
| |
|
|
|
|
| SOR() |
Natural |
72 (54) |
.356 (.280) |
.368 (.307) |
| |
Red-black |
65 (47) |
.311 (.224) |
.469 (.411) |
| |
|
|
|
|
| SSORCG() |
Natural |
17 (13) |
.232 (.173) |
.264 (.185) |
| |
|
|
|
|
| SSORSI() |
Natural |
23 (22) |
.242 (.213) |
.273 (.244) |
| |
|
|
|
|
| RSCG() |
Red-black |
31 (31) |
.104 (.117) |
.269 (.297) |
| |
|
|
|
|
| RSSI() |
Red-black |
60 (48) |
.207 (.166) |
.358 (.344) |
|
Table 2:
Number of Iterations and Execution Times for
Problem (2) Using Adaptive and Nonadaptive
Procedures (Nonadaptive Data in Parentheses)
| Routine |
Ordering |
Iterations |
Iteration time |
Total time |
| JCG() |
Natural |
28 (28) |
.092 (.090) |
.107 (.090) |
| |
Red-black |
28 (28) |
.079 (.074) |
.191 (.202) |
| |
|
|
|
|
| JSI() |
Natural |
64 (54) |
.166 (.136) |
.196 (.152) |
| |
Red-black |
64 (54) |
.160 (.130) |
.268 (.266) |
| |
|
|
|
|
| SOR() |
Natural |
42 (29) |
.139 (.095) |
.150 (.110) |
| |
Red-black |
38 (29) |
.124 (.097) |
.236 (.231) |
| |
|
|
|
|
| SSORCG() |
Natural |
15 (11) |
.136 (.097) |
.167 (.111) |
| |
|
|
|
|
| SSORSI() |
Natural |
19 (15) |
.138 (.101) |
.153 (.117) |
| |
|
|
|
|
| RSCG() |
Red-black |
15 (15) |
.032 (.051) |
.150 (.169) |
| |
|
|
|
|
| RSSI() |
Red-black |
31 (27) |
.075 (.064) |
.186 (.196) |
|
Values corresponding to the red-black ordering with the SSOR methods
are omitted from the tables since it is known that these methods are
ineffective with this ordering. Since the RS methods are defined for
only the red-black ordering, the table entries for these methods with
the natural ordering are not included.



Next: Notes on Use
Up: ITPACK 2C: A FORTRAN
Previous: Examples
![]() , we obtain a sparse linear system with 1729 nonzero
elements and 361 unknowns.
, we obtain a sparse linear system with 1729 nonzero
elements and 361 unknowns.
![]()
![]()
![]()