Main page
Chapter 10: Parametric Equations and Polar Coordinates
Chapter 12: Vectors and the Geometry of Space
Chapter 13: Vector Functions
Learning module LM 13.1/2: Vector valued functions
Learning module LM 13.3: Velocity, speed and arc length:
Learning module LM 13.4: Acceleration and curvature:
Tangent and normal vectorsCurvature and acceleration
Kepler's laws of planetary motion
Worked problems
Chapter 14: Partial Derivatives
Chapter 15: Multiple Integrals
Kepler's laws of planetary motion
|
Kepler's Laws: given the enormous impact Kepler's Laws of planetary
motion (circa 1609) and Newton's mathematical derivation of them in 1687, it's
worth seeing what they say. Kepler arrived at his three laws by the
first example of 'data-mining'. He took the detailed astronomical
observations made by Tycho Brahe over a period of many years and
extracted the Laws from this 'data-set'. By contrast, Newton
invented calculus, then formulated his three Laws of Motion, and
finally arrived at what we would now call a differential equation
from which he derived Kepler's Laws.
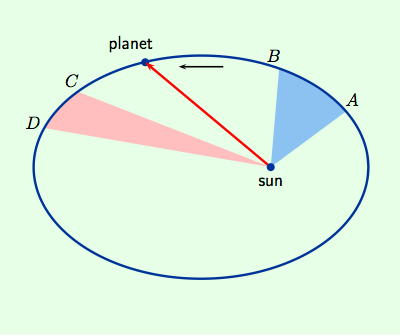
Recall that an ellipse is the set of all points $P$ such that the sum $$\hbox{dist}\{P,\,F_1\}+ \hbox{dist}\{P,\,F_2\}$$ of the distances from foci $F_1,\, F_2$ is constant. As shown to the right, take one of these foci as origin and place the sun there; then parametrize the orbit of a planet by ${\bf r} (t)$. |
|
Kepler's Laws:
 The orbit of a planet is an ellipse with the sun at one focus.
The orbit of a planet is an ellipse with the sun at one focus.
 The position vector ${\bf r}(t)$ from the sun to the planet sweeps out equal areas in equal times.
The position vector ${\bf r}(t)$ from the sun to the planet sweeps out equal areas in equal times.
 The square of the period of revolution of the planet about the sun is proportional to the cube of the length of the semi-major axis of its orbit.
The square of the period of revolution of the planet about the sun is proportional to the cube of the length of the semi-major axis of its orbit.
|
The blue and pink regions above have equal area to illustrate the Second Law, for instance. On the other hand, in vector form Newton's Second Law of Motion says that ${\bf F} = m {\bf a}$ where ${\bf F}$ is the net force vector acting on an object and ${\bf a}$ is its acceleration. In the case of planetary motion, Newton's Law of Gravitation says that the sun attracts the planet with a gravitational force of magnitude $G M m / \|{\bf r}(t)\|^2$ in the direction of the vector $-{\bf r}(t)$ where ${\bf r}(t)$ is shown above and $G,\, m,\, M$ are various constants like mass. Thus $${\bf F} ({\bf r}(t) )\ = \ -\Big(\frac{GMm}{\|{\bf r}(t)\|^2}\Big) \frac{{\bf r}(t)}{\|{\bf r}(t)\|} \ = \ - \frac{GMm}{\|{\bf r}(t)\|^3} \, {\bf r}(t)\,.$$ But by Newton's Second Law of Motion, ${\bf F} ({\bf r} (t)) = m {\bf r}''(t)$. So he arrived at the differential equation $${\bf r}''(t) \ = \ - \frac{\hbox{const}}{\|{\bf r}(t)\|^3} {\bf r}(t)\,.$$ By solving this equation for ${\bf r}(t)$, we, like Newton, can derive each of Kepler's Laws.
In fact we have already developed most of the math needed. To understand the equal-areas law, think about how much area is swept out in a short time $\Delta t$. This is essentially a triangle with vertices at the origin, at ${\bf r}(t)$, and at ${\bf r}(t + \Delta t)$, and so has area $$\frac{1}{2} \| {\bf r}(t) \times [{\bf r}(t+\Delta t)-{\bf r}(t)]\| \approx \frac{\Delta t}{2} \|{\bf r}(t) \times {\bf r}'(t)\|\,.$$ To prove the equal-areas law, we just have to show that $\| {\bf r} \times {\bf r}'\|$ is constant. In fact, something even stronger is true: the vector ${\bf r} \times {\bf r}'$ is constant: $$\frac{d}{dt}[{\bf r} \times {\bf r}'] = {\bf r}' \times {\bf r}' + {\bf r} \times {\bf r}''.$$ The first term is obviously zero, since the cross product of any vector with itself is zero. The second term is also zero, since ${\bf r}''$ points in the same direction as $-{\bf r}$.
The quantity $m {\bf r} \times {\bf r}'$ is called the angular momentum of the orbiting object. Since the force (and acceleration) is in the ${\bf r}$ direction, the angular momentum is conserved. Since the angular momentum is constant, the object sweeps out equal areas in equal times.
Proving that the orbits are ellipses, and the relation between the period and the semi-major axis, is a bit trickier, and is best left to a class on differential equations or physics or astronomy.