Absolute maxima

Definition: If $(a, \,b)$ is a point in a region $D$ in the $xy$-plane, then $z=f(x, \,y)$ is said to have      an Absolute Maximum on $D$ at $(a,\,b)$ when $f(x, \,y) \le f(a, \,b)$ holds for all $(x,\, y)$ in $D$,      an Absolute Minimum on $D$ at $(a,\,b)$ when $f(x, \,y) \ge f(a, \,b)$ holds for all $(x,\, y)$ in $D$. Absolute maxima and minima are also called Global maxima and minima.

Theorem: An absolute maximum (resp. absolute minimum) of $z = f(x,\,y)$ on $D$ occurs at a critical point inside $D$ or at a point on the Boundary of $D$.

The reason is the same as in one dimension. If you have a point in the interior where $\nabla f \ne 0$, then you can get to a larger value of $f$ by moving in the $\nabla f$ direction, and get to a smaller value by moving in the $-\nabla f$ direction. If you keep moving in the $\nabla f$ direction, you will either approach a critical point, or you will hit the boundary.

Our strategy to find absolute maxima and minima is

1. Find the critical points on the interior. This involves computing $\nabla f(x,\,y)$ and setting it equal to zero.
2. Maximize (or minimize) $f(x,\,y)$ on the boundary.
3. Compare the values of $f(x,\,y)$ that you found from the first two steps. Whichever is biggest is the absolute maximum.
4. Likewise, whichever is smallest is the absolute minimum.

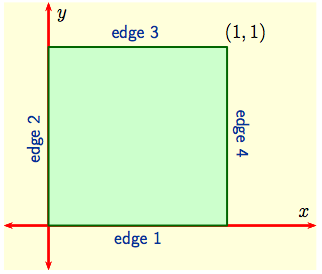
Example 1: Determine the absolute minimum value of $$f(x,\, y) \ = \ x + 3y - 4xy$$ on the unit square shown in Solution: First we find the critical points of $$f(x,\, y) \ = \ x + 3y - 4xy\,.$$ Now $$\frac{\partial f}{\partial x} \,=\,1 - 4y \,=\, 0,\quad \frac{\partial f}{\partial y} \,=\,3 - 4x\,=\,0\,,$$

so the only critical point is $\bigl(\frac{3}{4},\, \frac{1}{4}\bigl)$, and this lies inside the unit square. At this critical point, $$f\Bigl(\frac{3}{4}\,, \ \frac{1}{4}\Bigr) \ = \ \frac{3}{4}\,.$$ Next we look at the behavior of $f$ on the four edges separately, since the minimum value of $f$ on the boundary must be the minimum value on one of the edges.: Edge 1: here $y = 0,\, 0\le x \le 1$, and $$\min_{0\le x\le 1}\, f(x,\,0) \ = \ \min_{0\le x\le 1}\, x \ = \ 0\,.$$ Edge 2: here $x = 0,\, 0\le y \le 1$, and $$\min_{0\le y\le 1}\, f(0,\,y) \ = \ \min_{0\le y\le 1}\, 3y \ = \ 0\,.$$ Edge 3: here $y = 1,\, 0\le x \le 1$, and $$\min_{0\le x\le 1}\, f(x,\,1) \ = \ \min_{0\le x\le 1}\, (3-3x) \ = \ 0\,.$$ Edge 4: here $x = 1,\, 0\le y \le 1$, and $$\min_{0\le y\le 1}\, f(1,\,y) \ = \ \min_{0\le y\le 1}\, (1-y) \ = \ 0\,.$$ Consequently, on the unit square $f$ has $$\hbox{Abs Min Value} \ = \ \min \Bigl\{\, \frac{3}{4},\ 0,\ 0, \ 0,\ 0\, \Bigl\} \ = \ 0 \,.$$

In Example 1 the extrema on the boundary could be determined by straightforward inspection. In other cases we need to use the max/min methods we learned for functions of one variable.

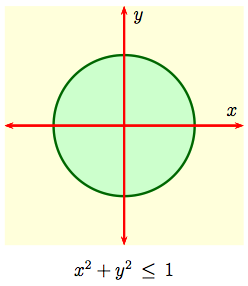
Example 2: Find the absolute maximum and minimum values of $$f(x,\, y) \ = \ x^2 + y^2 - x - y +1$$ on the unit disk $$D \ = \ \big\{(x,\,y): x^2 + y^2 \le 1\big\}\,. $$ Solution: The absolute maximum and minimum values occur either at a critical point inside the disk, i.e., in the region $\{ (x,\,y) : x^2 + y^2 < 1\}$, or on the boundary of the disk, i.e., on the circle $\{ (x,\,y) : x^2 + y^2 = 1\}$. We first find the critical points: when $$f(x,\, y) \ = \ x^2 + y^2 - x - y +1\,,$$ then $$\frac{\partial f}{\partial x} \,=\,2x -1\,,\quad \frac{\partial f}{\partial y} \,=\,2y - 1\,=\,0\,.$$ So $(1/2,\,1/2)$ is the only critical point, and this lies inside the disk. At this critical point $$f\Big(\frac{1}{2},\ \frac{1}{2}\Big) \ = \ \frac{1}{2}\,.$$ We next look at the behavior of $f$ on the boundary.

Since this is the circle $${\bf r}(t) \ = \ \cos t \, {\bf i} + \sin t \, {\bf j} \,, \quad 0 \le t \le 2\pi\,,$$ the restriction of $f$ to the boundary is the function $$f({\bf r} (t)) \ = \ 1 - \cos t - \sin t + 1\qquad \qquad$$ $$\qquad = \ 2 -\cos t - \sin t\,.$$ Finding the absolute extrema of $f({\bf r} (t))$ on $[0,\,2\pi]$ is a single variable problem: the absolute extrema will occur either at a critical point in $(0,\,2\pi)$, or at the endpoints $t=0,\,2\pi$. But $$\frac{d}{dt}\,f({\bf r} (t)) \ = \ \sin t - \cos t\,,$$ so the critical points of $f({\bf r} (t))$ on $(0,\,2\pi)$ occur at $t = \pi/4,\, 5\pi/4$. But $$f\Big({\bf r} \Big(\frac{\pi}{4}\Big) \Big)= 2 - \sqrt{2}, \ f\Big({\bf r} \Big(\frac{5\pi}{4}\Big) \Big) = 2+ \sqrt{2}\,,$$ while $$f({\bf r} (0)) \ = \ 1,\quad f({\bf r} (2\pi)) \ = \ 1\,.$$ Thus $$\max_D\, f(x,\,y) = 2+ \sqrt{2}\,, \ \ \min_D\,f(x,\,y)=\frac{1}{2}\,.$$